Lösungshinweise Aufgabe 35 b
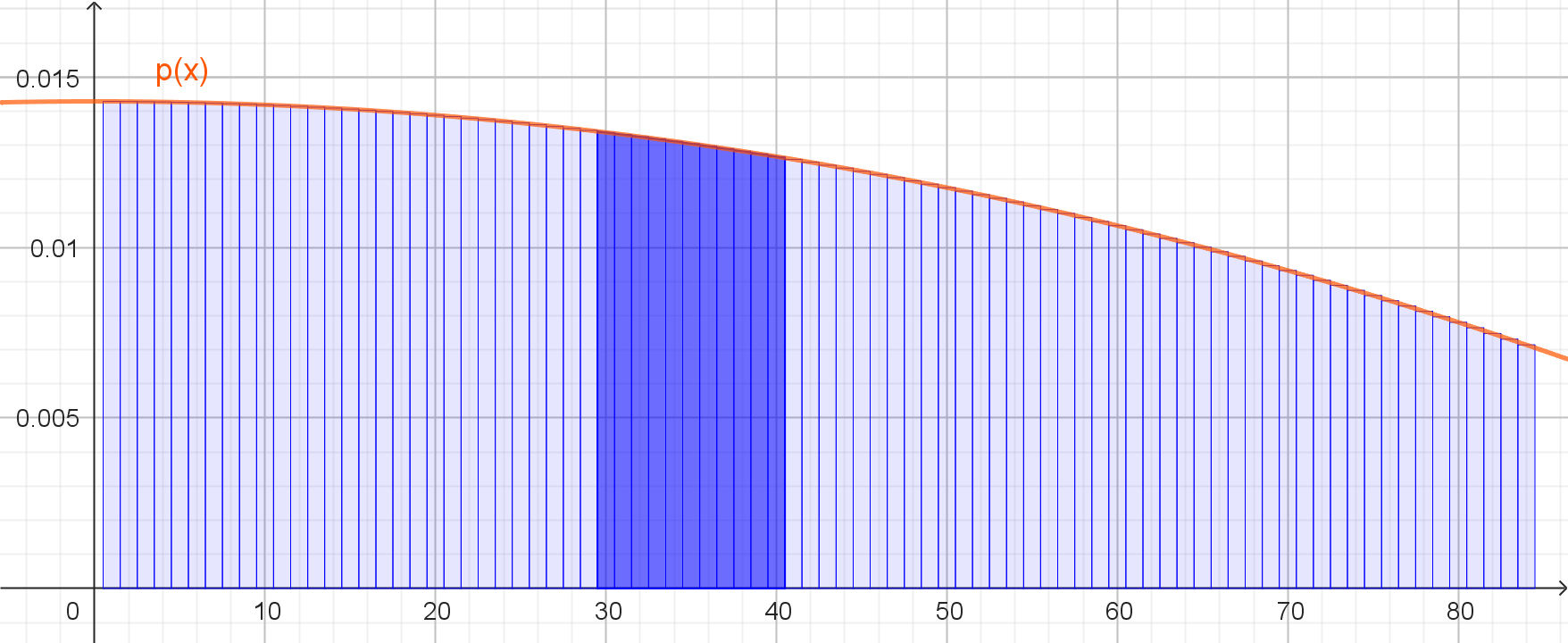
Die Wahrscheinlichkeit dafür, dass Max sich irgendwo zwischen der 29. und
der 41. Etage, also mindestens in der 30. und höchstens in der 40. Etage
aufhält, wird durch das Integral
\(
\int \limits_{30-0,5}^{40+0,5}p(x) dx
\)
berechnet. Also
\(\begin{align}
&\int \limits_{30-0,5}^{40+0,5}
\left( \frac{1}{70}\cdot
\left(
1 - 0,5 \cdot \left(\frac{x}{84}\right)^2
\right)
\right) dx \\
=\frac{1}{70}\cdot &\int \limits_{29,5}^{40,5}
\left(
1 - 0,5 \cdot \frac{x^2}{84^2}
\right) dx \\
=\frac{1}{70}\cdot
&\left[
1 \cdot x - 0,5 \cdot \frac{x^3}{84^2}
\right]_{29,5}^{40,5} \\
=\frac{1}{70}\cdot
&\left[
\left(1 \cdot 40,5 - 0,5 \cdot \frac{40,5^3}{84^2}\right)
-
\left(1 \cdot 29,5 - 0,5 \cdot \frac{29,5^3}{84^2}\right)
\right] \\
\approx 0,143 &
\end{align}\)
Die gesuchte Wahrscheinlichkeit beträgt also ungefähr 14,3%.