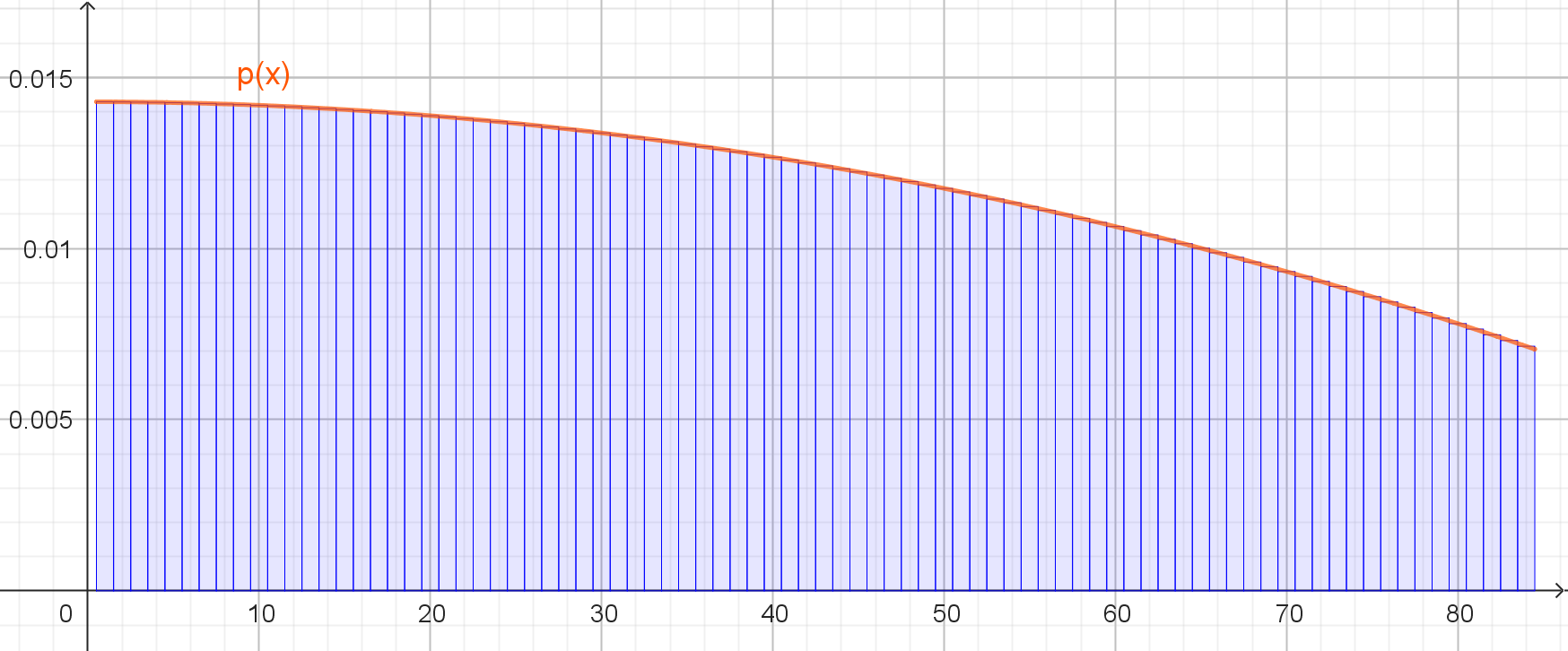
Lösungshinweise Aufgabe 35 a
Die Funktion für die Wahrscheinlichkeit ist mit
\(\begin{align}
p(x)=\frac{1}{70}\cdot \left(1 - 0,5\cdot \left(\frac{x}{84} \right)^2 \right)
\end{align}\)
gegeben.
Dann ist
\(\begin{align}
p(84)&=\frac{1}{70}\cdot \left(1 - 0,5\cdot \left(\frac{84}{84} \right)^2 \right)\\
&=\frac{1}{70}\cdot \left(1 - 0,5\cdot 1^2 \right)\\
&=\frac{1}{70}\cdot 0,5\\
&\approx 0,00714
\end{align}\)
und
\(\begin{align}
p(1)&=\frac{1}{70}\cdot \left(1 - 0,5\cdot \left(\frac{1}{84} \right)^2 \right)\\
&=\frac{1}{70}\cdot \left(1 - 0,5\cdot \frac{1}{7056} \right)\\
&=\frac{1}{70}\cdot \left(1 - 0,000\,07086 \right)\\
&\approx \frac{1}{70}\cdot 1\\
&\approx 0,01428
\end{align}\)
Damit ist gezeigt, dass p(x)
an der Selle 84 ziemlich genau halb so groß ist wie an der Stelle 0.