Hinweis zu Aufgabe 34b
| k | P(X = k) |
|---|---|
| 1 | 20% |
| 2 | 17% |
| 3 | 17% |
| 4 | 17% |
| 5 | 17% |
| 6 | 12% |
- Berechnen Sie die Wahrscheinlichkeit dafür, dass bei 100 Würfen genau 20-mal die 1 gewürfelt wird.
Hier geht es also nur um das Werfen einer 1, und die erscheint
laut Tabelle immer mit der Wahrscheinlichkeit 0,2.
Im Gegensatz zu Aufgabenteil b) liegt bei dieser Fragestellung
eine Binomialverteilung
vor.
Es ist \(\,n=100\,\) und \(\,p=0,2\,\).
Die Zufallsgröße X bescheibt jetzt nicht die
Augenzahl, sondern die Anzahl der Einsen beim 100-fachen Wurf.
Gesucht ist nun
\(
P(X=20)
\).
Die Formel zur Berechnung lautet
\[\begin{align}
P(X=k)\;&=\;\pmatrix{n \\k}\cdot p^k \cdot (1-p)^{n-k}\\
&=\;\pmatrix{100\\20}\cdot 0,2^{20}\cdot 0,8^{80}\\
&=0,0993
\end{align}\]
Sie können diesen Wert mit dem Taschenrechner auch direkt über den
Menüpunkt Binomial-Dichte berechnen.
Achten Sie darauf, nicht die
kumulierte Binom.-Vert. auszuwählen. Hier geht es ja nicht um die
Wahrscheinlichkeit für den Bereich von 0 bis 20, sondern nur um
die Wahrscheinlichkeit für den einen Wert X=20
- Berechnen Sie die Wahrscheinlichkeit dafür, dass bei 100 Würfen höchstens 16-mal die 1 gewürfelt wird.
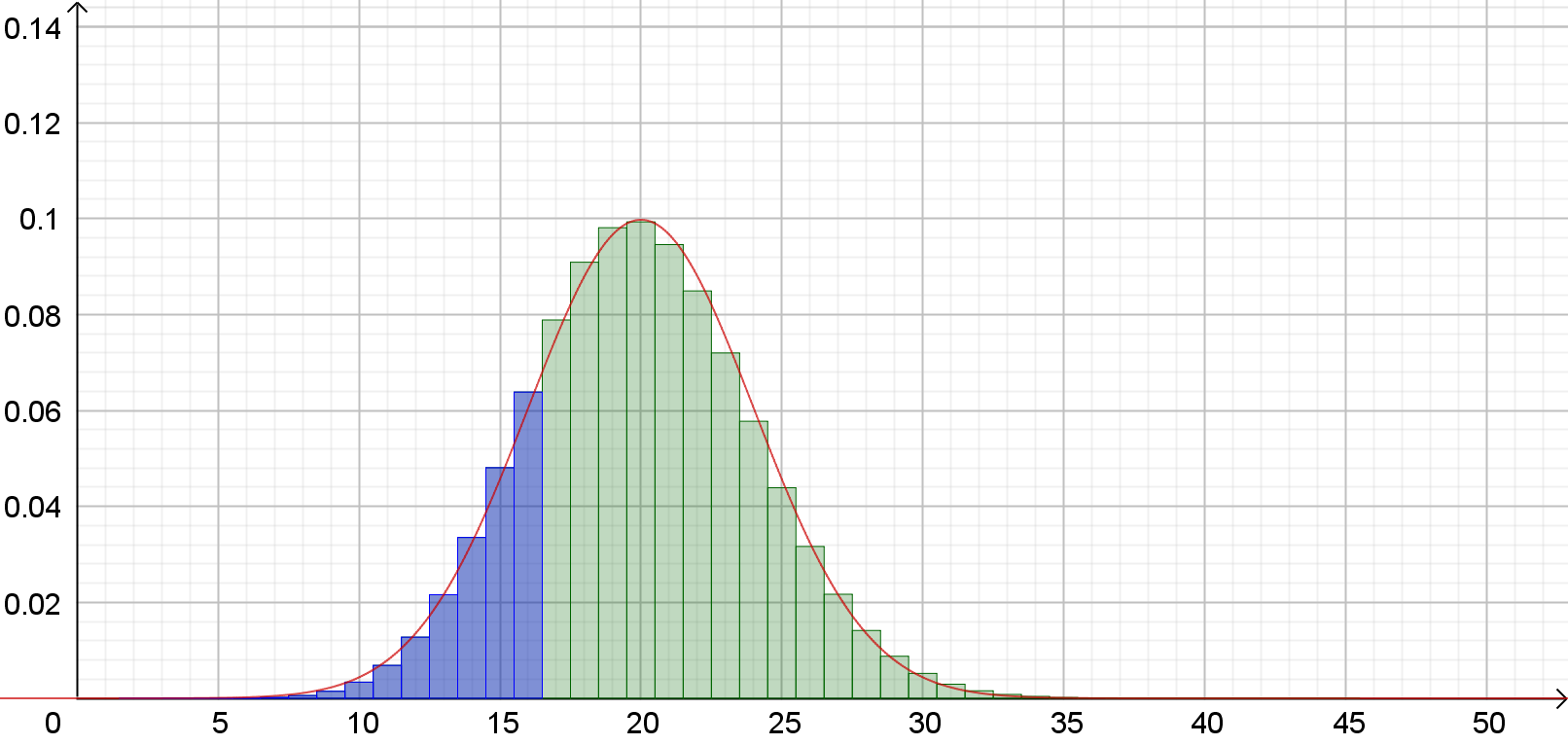
Hier ist die kumulierte Wahrscheinlichkeit
P(X ≤ 16) gesucht.
Meine Lösung ist \(P(X\le 16)\;\approx\; 0,192\).
die Wahrscheinlichkeit dafür, höchstens 16 Einsen unter
den 100 Würfen zu haben, ist also ungefähr 19,2%. Dies entspricht dem
blau eingefärbten Bereich im abgebildeten Histogramm.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass bei 100 Würfen mindestens 10-mal eine 6 gewürfelt wird.
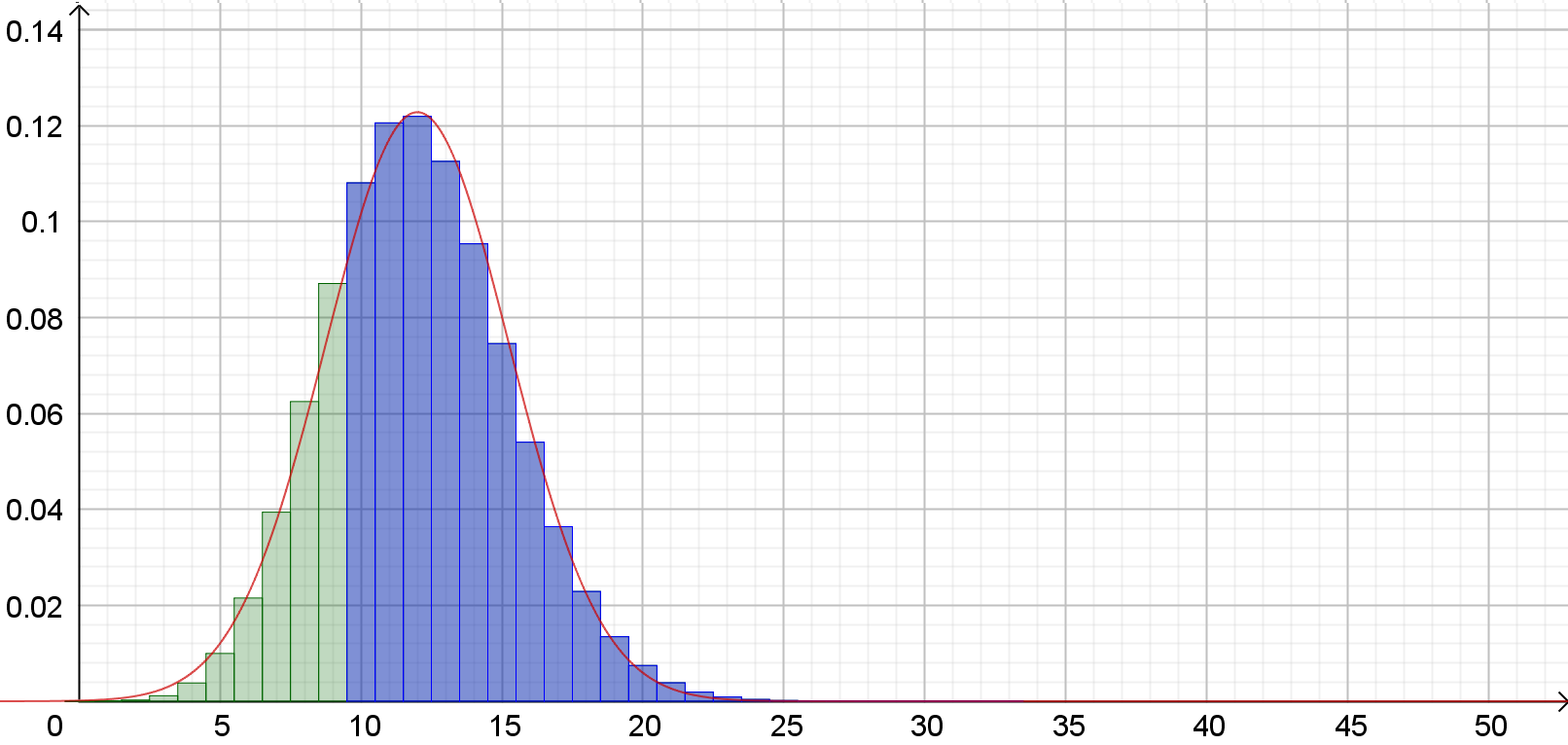
Jetzt geht es um das Würfeln einer 6, die Wahrscheinlichkeit dafür
ist 0,12.
Die in der Abbildung blau eingefärbte Fläche entspricht dieser
Wahrscheinlichkeit.
Gesucht ist
P(X ≥ 10):
\(\begin{align}
P(X\ge 10)\;&=\;1 - P(X\le 9)\;\\
&\approx\; 1 - 0,226\\
&\approx\; 0,774
\end{align}\)
Mit einer Wahrscheinlichkeit von 77,4% werden bei 100 Würfen mindestens 10 Sechsen gewürfelt.