Lösung zu Aufgabe 29d
Die Gauß-Funktion und ihre Ableitung sind \[ \varphi(x) =\frac{1}{\sqrt{2\pi}}\cdot \large{e^{\Large{-\frac{x^2}{2}}}} \] \[ \varphi'(x) =-x \cdot \frac{1}{\sqrt{2\pi}}\cdot \large{e^{\Large{-\frac{x^2}{2}}}} = -x \cdot \varphi(x) \] Die zweite Ableitung ist nach der Produktregel \[ \begin{align} \varphi''(x) &= -1 \cdot \varphi(x) ~+~ (-x) \cdot \varphi'(x)\\ &= -1 \cdot \varphi(x) ~+~ (-x) \cdot (-x \cdot \varphi(x))\\ &= -1 \cdot \varphi(x) ~+~ x^2 \cdot \varphi(x)\\ &= (-1+x^2)\cdot \varphi(x)\\ &= (x^2-1)\cdot \varphi(x) \end{align}\] Wenn man den Term für \(\varphi''(x)\) so wie hier mit Hilfe von \(\varphi(x)\) ausdrückt, ist die Darstellung übersichtlicher als es mit Bruch, Wurzel und Exponentialfuntktion gewesen wäre.
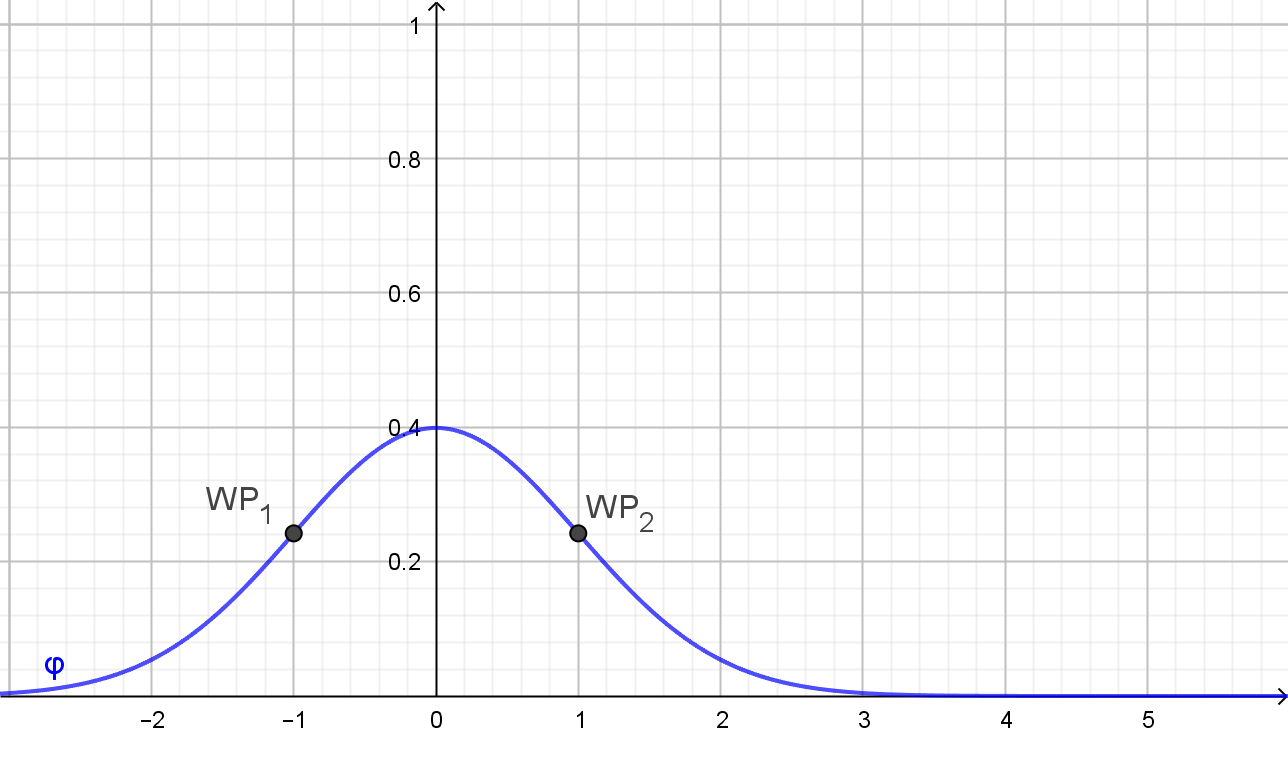
Notwendige Bedingung für einen Wendepunkt an der Stelle \(x\) ist \(\varphi''(x)=0\). Das bedeutet aber \( (x^2-1) = 0\), denn \(\varphi(x)\) wird niemals 0. \[ x^2-1=0 ~\Leftrightarrow~ x=-1 ~\vee~ x=+1 \] Wendepunkte kann es also nur bei x=+1 und bei x=−1 geben.
Ohne Berechnung der dritten Ableitung kann begründet werden, dass
bei diesen beiden Stellen ein Wendepunkt vorliegt, weil die zweite
Ableitung an diesen beiden Stellen ihr Vorzeichen ändert:
Für \(-1 < x < +1\) ist \(x^2 < 1 \) uns somit \(x^2-1\) negativ.
Ist dagegen \(x < -1 \) oder \(x > +1 \) ist \(x^2-1\) positiv.
Alternativ könnte man auch die dritte Ableitung berechnen, sie ist \[ \varphi'''(x) = (-x^3 + 3 x) \cdot \varphi(x) \] Da sowohl \(\varphi'''(-1) \ne 0\) als auch \(\varphi'''(+1) \ne 0\) gilt, liegen an beiden Stellen Wendepunkte.
Die \(y\)‑Koordinate der Wendepunkte sind
\(
\varphi(\pm 1)=\frac{1}{\sqrt{2\pi}}\cdot
\large{e^{\Large{-\frac{1}{2}}}}
\approx
0,24197
\approx
0,242
\)
Also sind WP1(-1|0,242) und WP2(1|0,242) die
Wendepunkte.