Lösung zu Aufgabe 29c
Die Gauß-Funktion
\[
\varphi(x) =\frac{1}{\sqrt{2\pi}}\cdot
\large{e^{\Large{-\frac{x^2}{2}}}}
\]
wird mit Hilfe der Kettenregel abgeleitet.
Der konstante Faktor \(\frac{1}{\sqrt{2\pi}}\) bleibt erhalten.
Die Ableitung der \(e\)-Funktion ist wieder die \(e\)-Funktion mit demselben
Argument
\(-\frac{x^2}{2}\).
Nach der Kettenregel muss schließlich noch mit der Ableitung der inneren
Funktion, also mit der Ableitung von \(-\frac{x^2}{2}\), multipliziert
werden. Diese Ableitung ist \(-x\).
Die gesamte Ableitung lautet also
\[
\varphi'(x) =\frac{-x}{\sqrt{2\pi}}\cdot
\large{e^{\Large{-\frac{x^2}{2}}}}
\]
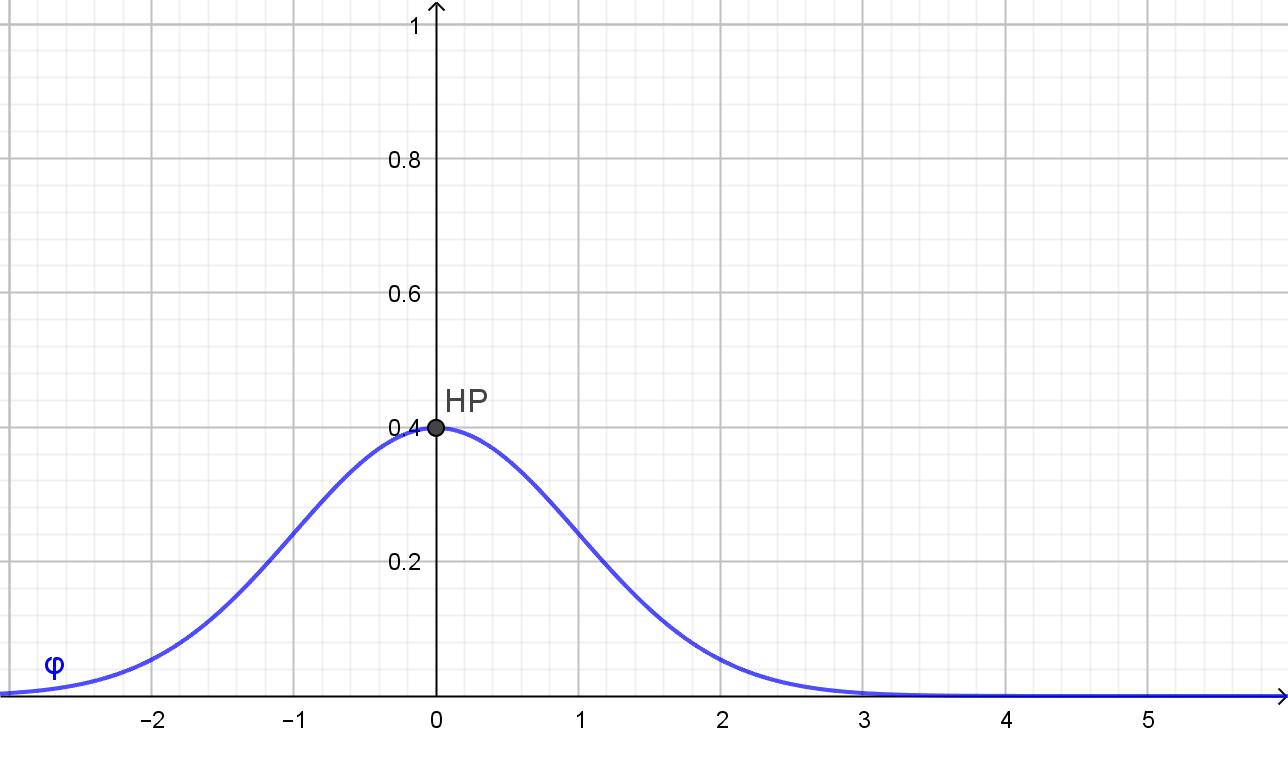
Notwendige Bedingung für ein Extremum an der Stelle \(x\) ist \(\varphi'(x)=0\). Das bedeutet aber \( x=0\), denn die Exponentialfunktion wird niemals 0.
Ohne Berechnung der zweiten Ableitung kann begründet werden, dass
bei \( x=0\) ein Extremum in Form eines Hochpunktes vorliegt:
Die Ableitung von \(\varphi\) ist dort 0, für negative \(x\)‑Werte
ist die Ableitung positiv, und für positive \(x\)‑Werte ist die
Ableitung negativ.
Das bedeutet aber, dass die Funktion \(\varphi(x)\) für \(x<0\)
steigend und für \(x>0\) fallend verläuft.
Somit liegt bei \(x=0\) ein Hochpunkt.
Alternativ könnte man auch die zweite Ableitung berechnen, siehe Hinweise zu Teil d). \(\varphi''(x)\) ist bei \(x=0\) negativ und daraus folgt, dass bei \(x=0\) ein Hochpunkt liegt.
Die \(y\)‑Koordinate des Hochpunktes ist
\(
\varphi(0)=\frac{1}{\sqrt{2\pi}}\cdot
\large{e^{\Large{-\frac{0^2}{2}}}}
\normalsize=\frac{1}{\sqrt{2\pi}}\cdot 1
\approx
0,39894
\approx
0,40
\)
Also ist HP(0|0,4) der Hochpunkt.