Lösungshinweise Aufgabe 13: Varianz
Die Berechung der Varianz wird einfach, wenn man die Tabelle zur
Berechnung des Erwartungswerts um zwei Spalten erweitert:
Zunächst wird eine Spalte ergänzt, in der die Differenz zum Mittel- oder
Erwartungwert erfasst wird.
Dann folgt eine Spalte für die Quadrate der Differenzen, die noch mit
der jeweiligen Wahrscheinlichkeit multipliziert werden.
| Hersteller B | ||||
|---|---|---|---|---|
| F | P(X=F) | F·P(X=F) | F−E(X) | [F−E(X)]2·P(X=F) |
| 925 N | 0 | 0 N | −220 N | 0 N2 |
| 975 N | 0,05 | 48,75 N | −170 N | 1445 N2 |
| 1025 N | 0,10 | 102,50 N | −120 N | 1440 N2 |
| 1075 N | 0,15 | 161,25 N | −70 N | 735 N2 |
| 1125 N | 0,25 | 281,25 N | −20 N | … N2 |
| 1175 N | 0,20 | 235,00 N | +30 N | … N2 |
| 1225 N | 0,10 | 122,50 N | +80 N | … N2 |
| 1275 N | 0,10 | 127,50 N | +130 N | … N2 |
| 1325 N | 0,05 | 66,25 N | +180 N | … N2 |
| Summe: | E(X) = 1145,00 N | \( V(X) = \) … N2 | ||
| Standardabweichung | \( S(X) = \sqrt{V(X)} = \)…N | |||
Die Differenzen in der 4. Spalte haben unterschiedliche Vorzeichen.
Ohne sie zu quadrieren würden sich negativen und positiven Abweichungen
vom Erwartungswert in der Summe weitgehend ausgleichen,
sodass kein brauchbares Maß für die Varianz entsteht.
Und natürlich muss berücksichtig werden, ob die jeweiligen Abweichungen
mit großer oder nur geringer Wahrscheinlichkeit auftreten, deshalb werden
die Abweichungsquadrate mit ihrer Wahrscheinlichkeit
multipliziert (5. Spalte).
Wenn die Zufallsgröße X eine
Maßeinheit hat, z.B. € oder N, so hat die Varianz dieselbe Einheit
im Quadrat, also z.B. €2 oder N2.
Deshalb wird die Varianz auch als die
mittlere quadratische Abweichung
bezeichnet.
Für die
Standardabweichung
wird die Wurzel aus der Varianz gezogen.
So erhält man eine Größe, die die gleiche Einheit wie der Erwartungswert
hat.
Die Standardabweichung wird gelegentlich mit
S(X)
bezeichnet, meistens jedoch mit dem griechischen Buchstaben σ (sigma).
Der Erwartungswert
E(X)
wird oft auch mit dem griechischen Buchstaben
μ (my) bezeichnet.
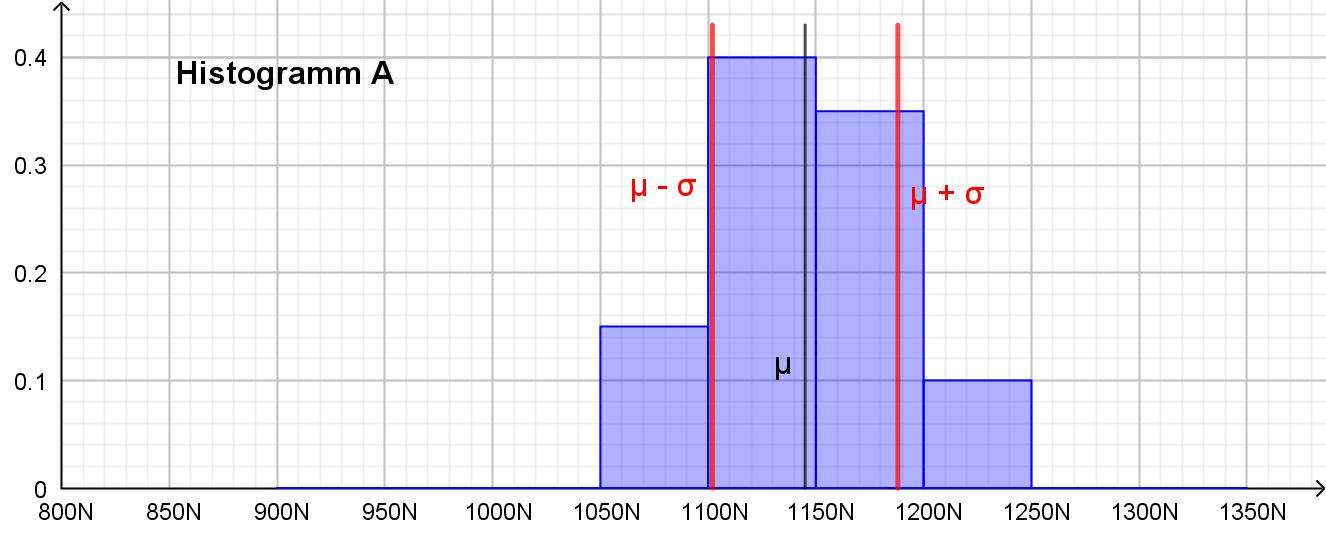
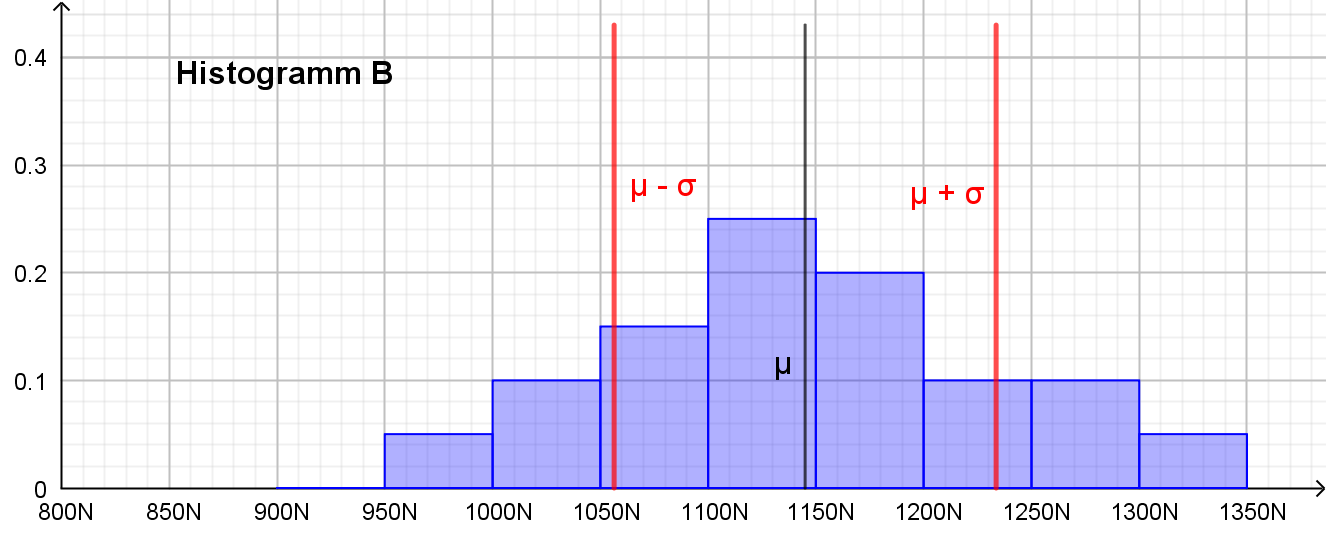
Der Mittel- oder Erwartungswert
μ=E(X)
ist für beide Schraubenhersteller der gleiche (hier durch die senkrechte Linie markiert.
Die mittlere Abweichung (Standardabweichung σ) vom Erwartungswert μ
ist im Histogramm durch die roten Linien markiert.