Lösungshinweise Aufgabe 11
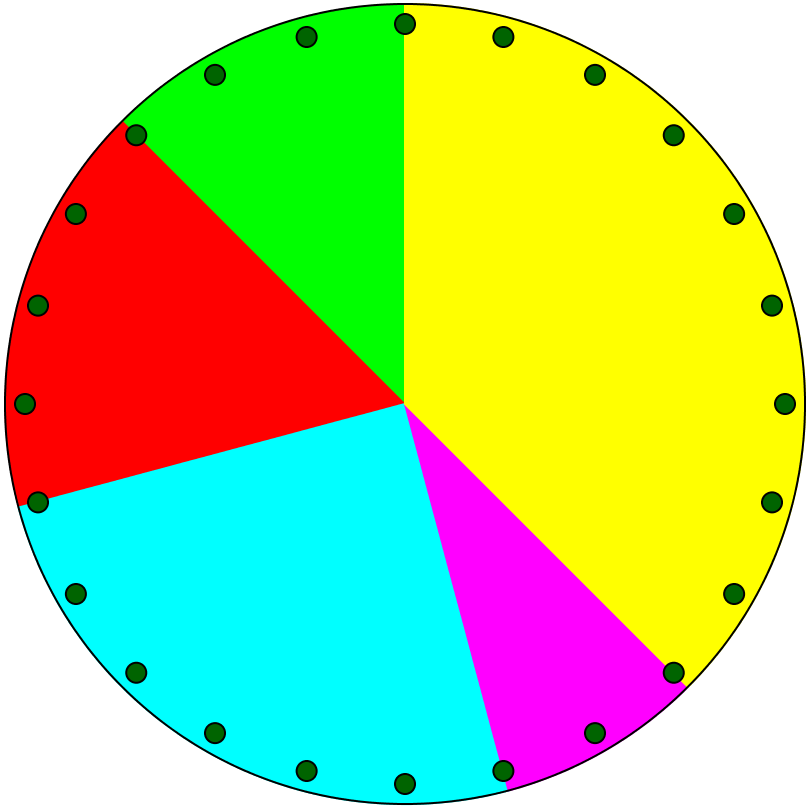
gelb: 0 €
blau: 1 €
rot: 2 €
grün: 4 €
mag.: 10 €
Die Wahrscheinlichkeiten sind die gleichen wie in Aufgabe 10, da das Glücksrad unverändert ist und nur der Gewinnplan anders ist.
| k | P(X = k) | k · P(X = k) |
|---|---|---|
| 0 € | 9⁄24 = 0,375 | 0 € · 9⁄24 = 0,00 € |
| 1 € | 6⁄24 = 0,25 | 1 € · 6⁄24 = 0,25 € |
| 2 € | 4⁄24 ≈ 0,167 | 2 € · 4⁄24 ≈ 0,33 € |
| 4 € | 3⁄24 = 0,125 | 4 € · 3⁄24 = 0,50 € |
| 10 € | 2⁄24 ≈ 0,083 | 10 € · 2⁄24 ≈ … € |
| Summen: | E(X) ≈ |
Sie haben richtig gerechnet, wenn Sie hier auf den gleichen Erwartungswert
für die Auszahlung kommen wie bei Aufgabe 10, nämlich auf
1,916 ≈ 1,92 €.
Bei 2 € Einsatz ist der mittlere Gewinn pro Spiel negativ,
anders ausgedrückt:
Der Erwartungswert für den Gewinn beträgt wieder ungefähr −0,08 €.
Obwohl bei beiden Spielen mit dem Glücksrad der gleiche Erwartungswert
vorliegt, sind die Spiele doch unterschiedlich.
Das wird deutlich, wenn man sich die zugehörigen
Histogramme
ansieht.
Ein Histogramm stellt die Wahrscheinlichkeiten
grafisch dar:
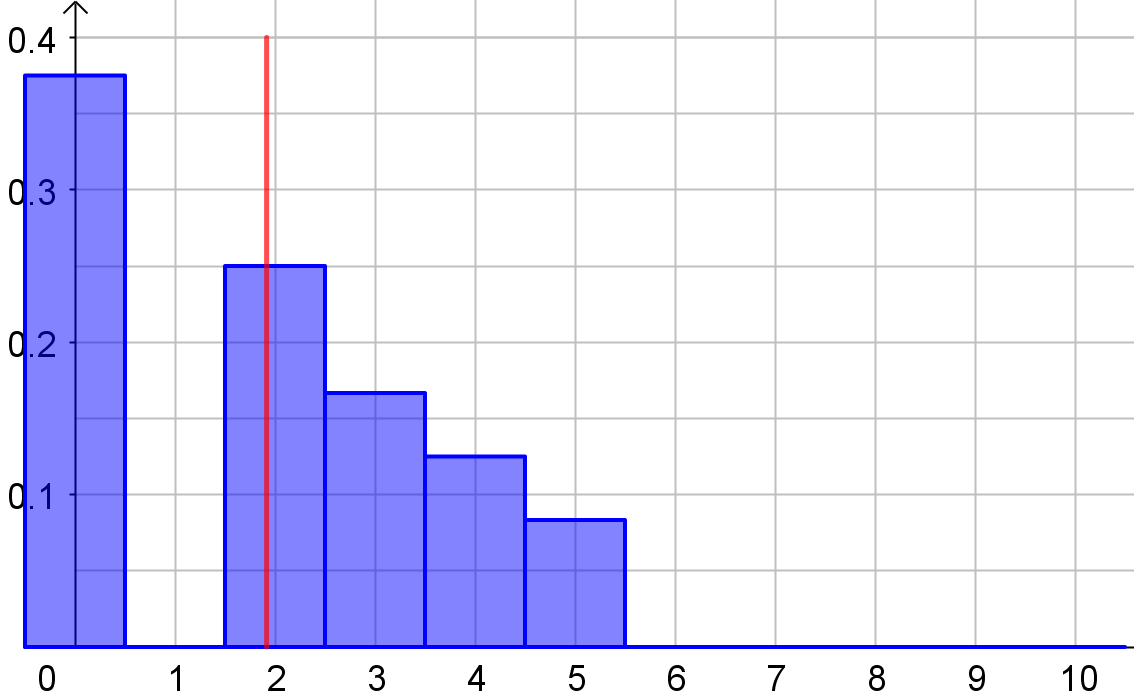
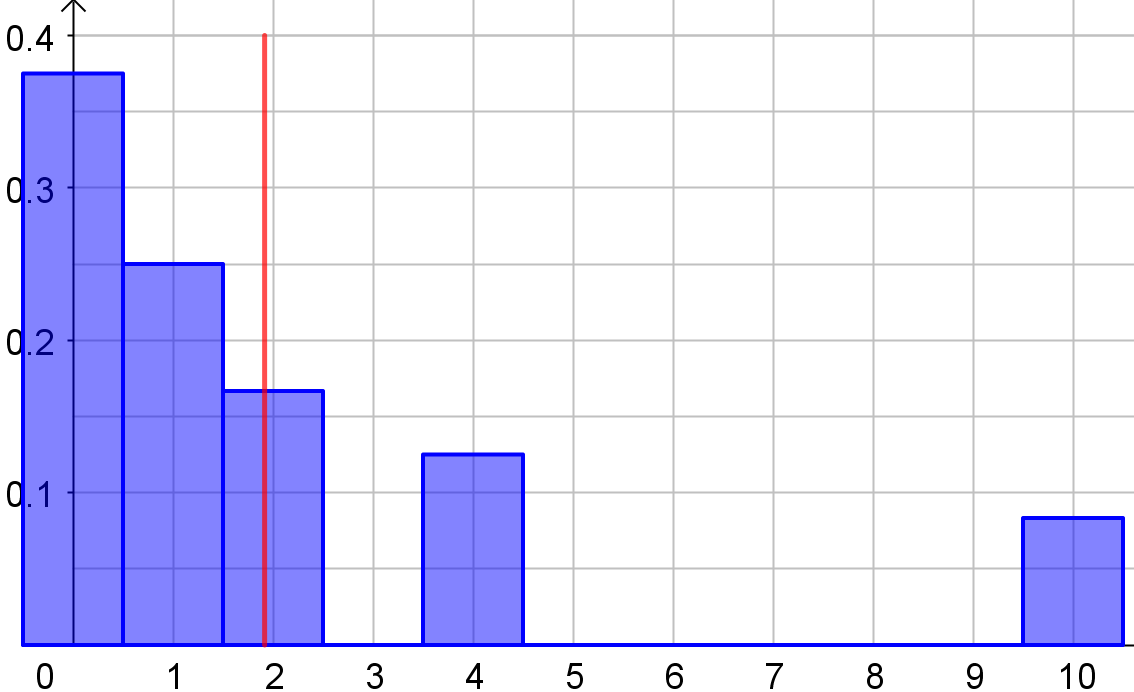
Der Mittel- oder Erwartungswert ist in beiden Fällen der gleiche (durch
die rote Linie markiert.
Bei dem zweiten Diagramm (Aufg. 11) nehmen die niedrigen Auszahlunge (0, 1, 2€)
einen größeren Bereich ein, dafür gibt es aber mit einer kleinen
Wahrscheinlichkeit die hohe Auszahlung von 10€.
Bei gleichem Erwartungswert würden risikobereite Spieler eher beim Glücksrad von Aufgabe 11 spielen, risikoscheue Spieler tendieren eher zum Glücksrad von Aufgabe 10.