Lösungshinweise zu Aufgabe 15 b
Die Aufhängepunkte der Kette liegen bei \(\left(\pm c \,\vert\, h\right)\) mit c=1 und h=0,57.
Die Funktionsgleichung lautet
\(
\quad f_a(x) = a\cdot \cosh \left(\frac{x}{a}\right) - a\cdot \cosh \left(\frac{c}{a}\right) + h
\)
Wenn \(\left(0 \,\vert\, d\right)\) der Schnittpunkt des Graphen mit der y‑Achse ist, muss gelten
\(
\quad d = a\cdot \cosh \left(\frac{0}{a}\right) - a\cdot \cosh \left(\frac{c}{a}\right) + h
\)
\(
\quad d = a\cdot \cosh \left(0\right) - a\cdot \cosh \left(\frac{c}{a}\right) + h
\)
\(
\quad d = a\cdot 1 - a\cdot \cosh \left(\frac{c}{a}\right) + h
\),
und nach Ausklammern von \(a\) und subtrahieren von d:
\(
\boxed{\quad a\left(1 - \cosh \left(\frac{c}{a}\right)\right) + h-d = 0}
\)
Mit den Werten c=1, h=0,57 und d=0,09 ergibt sich
\(
\quad a\left(1 - \cosh \left(\frac{1}{a}\right)\right) + 0,48 = 0
\)
Dieses ist die bestimmende Gleichung für den Parameter \(a\).
Sie kann nicht nach \(a\) aufgelöst werden.
Es gibt verschiedene Methoden, um eine Näherungslösung für \(a\) zu erhalten.
Im Grunde sucht man ja eine Nullstelle des Terms
\(
\quad a\left(1 - \cosh \left(\frac{1}{a}\right)\right) + 0,48
\)
Wenn man weiß, wie groß \(a\) ungefähr sein muss (nämlich etwas mehr als 1), kann man den Term
\(
\quad x\left(1 - \cosh \left(\frac{1}{x}\right)\right) + 0,48
\)
im Koordinatensystem für das Intervall \(0 \leq x \leq 2 \)
darstellen und ggf. danach noch einen kleineren Ausschnitt um die Nullstelle
genauer untersuchen:
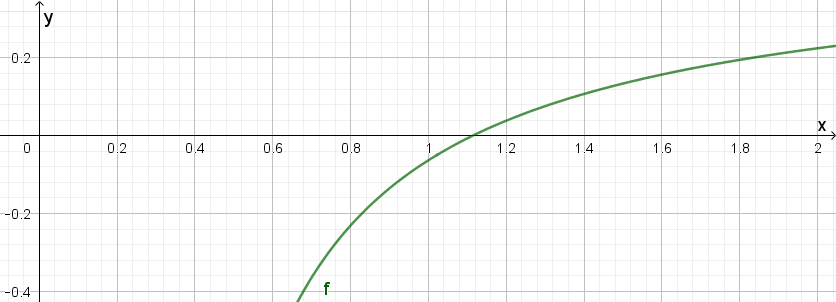
Hier ist zu erkennen, dass der gesuchte Wert für \(a\) zwischen 1,0 und 1,2 liegen muss, und zwar dicht bei 1,1.
Auf andere Methoden (CAS-Modul von GeoGebra, Taschenrechner Casio 991) wird im Aufgabentext mit Links verwiesen.