Lösungshinweise Aufgabe 14 d
Zu berechnen ist das Integral
\[
\ell = \int\limits_{a}^{b}\sqrt{1 + \left(f'(x)\right)^2}\;\text{d}x
\]
mit
\(f(x)=\cosh(x)\).
Nach Teilaufgabe b) ist
\(f'(x)=\cosh'(x) = \sinh(x)\).
Damit wird das zu berechnende Integral dann
\[
\ell = \int\limits_{a}^{b}\sqrt{1 + \sinh^2(x)}\;\text{d}x
\]
Aus
\(\quad\cosh^2(x) - \sinh^2(x) = 1 \)
folgt
\(\quad 1 + \sinh^2(x) = \cosh^2(x) \)
Damit vereinfacht sich das Integral zu
\[
\ell = \int\limits_{a}^{b}\sqrt{\cosh^2(x)}\;\text{d}x
\]
Der Term unter der Wurzel ist nicht nur wegen des Quadrierens auf dem gesamten
Definitionsbereich positiv.
Auch \(\cosh(x)\) hat ja an jeder Stelle \(x\) ein positives Vorzeichen (vgl. auch
die Funktionsgraphen).
Deshalb ist
\(\sqrt{\cosh^2(x)}=\cosh(x)\)
Damit vereinfacht sich das Integral noch weiter zu
\[
\ell = \int\limits_{a}^{b}\cosh(x)\;\text{d}x
\]
Nach der Formel im Text zu Teil b) ist \(\sinh(x)\) eine Stammfunktion zu \(\cosh(x)\).
Damit kann das Integral leicht berechnet werden:
\[
\begin{align}
\ell &= \int\limits_{a}^{b}\cosh(x)\;\text{d}x
= \left[\sinh(x) \right]_a^b\\
\ell &= \; \; \sinh(b) - \sinh(a)
\end{align}
\]
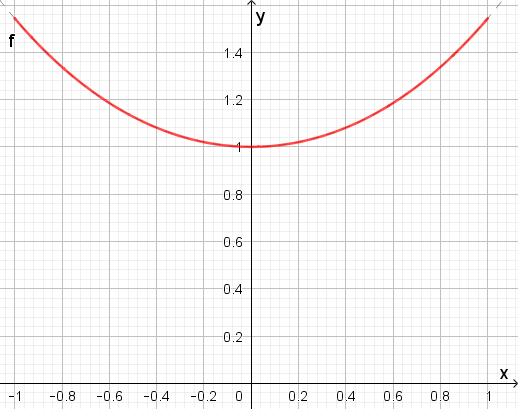
Nun zur Kurvenlänge im Intervall [−1; 1]:
\(
\begin{align}
\ell &= \int\limits_{-1}^{1}\sqrt{1 + \left(\cosh'(x)\right)^2}\;\text{d}x \\
&= \int\limits_{-1}^{1}\sqrt{1 + \left(\sinh(x)\right)^2}\;\text{d}x \\
&= \int\limits_{-1}^{1}\sqrt{\left(\cosh(x)\right)^2}\;\text{d}x \\
&= \int\limits_{-1}^{1}\cosh(x)\;\text{d}x = \left[\sinh(x)\right]_{-1}^{1} \\
&= \sinh(1) - \sinh(-1) \\
&\approx 1,175 - (-1,175) = 2,35
\end{align}
\)
Eine waagerecht von -1 bis +1 gespannte Kette hätte die Länge 2. Die durchhängende
Kette müsste etwas länger sein – insofern ist das berechnete Ergebnis plausibel.
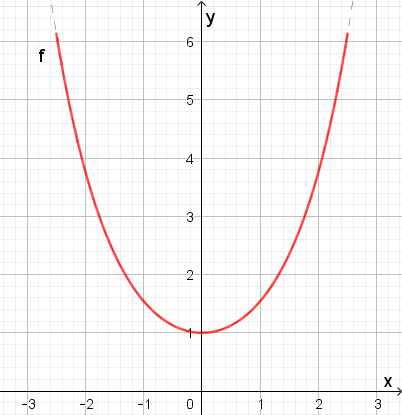
\( \begin{align} \ell &= \int\limits_{-2,5}^{2,5}\sqrt{1 + \left(\cosh'(x)\right)^2}\;\text{d}x \\ &= \sinh(2,5) - \sinh(-2,5) \\ &\approx 6,05 - (-6,05) = 12,1 \end{align} \)
Eine grobe Abschätzung für die Länge erhält man durch das das Doppelte der Strecke von
P(0|1) zu Q(2,5|6).
Das wäre nach Pythagoras ca. 11,2 und somit
steht auch hier die Berechnung der Kurvenlänge mit Hilfe des Integrals
in Einklang mit der Abschätzung.