Lösungshinweise Aufgabe 13 e
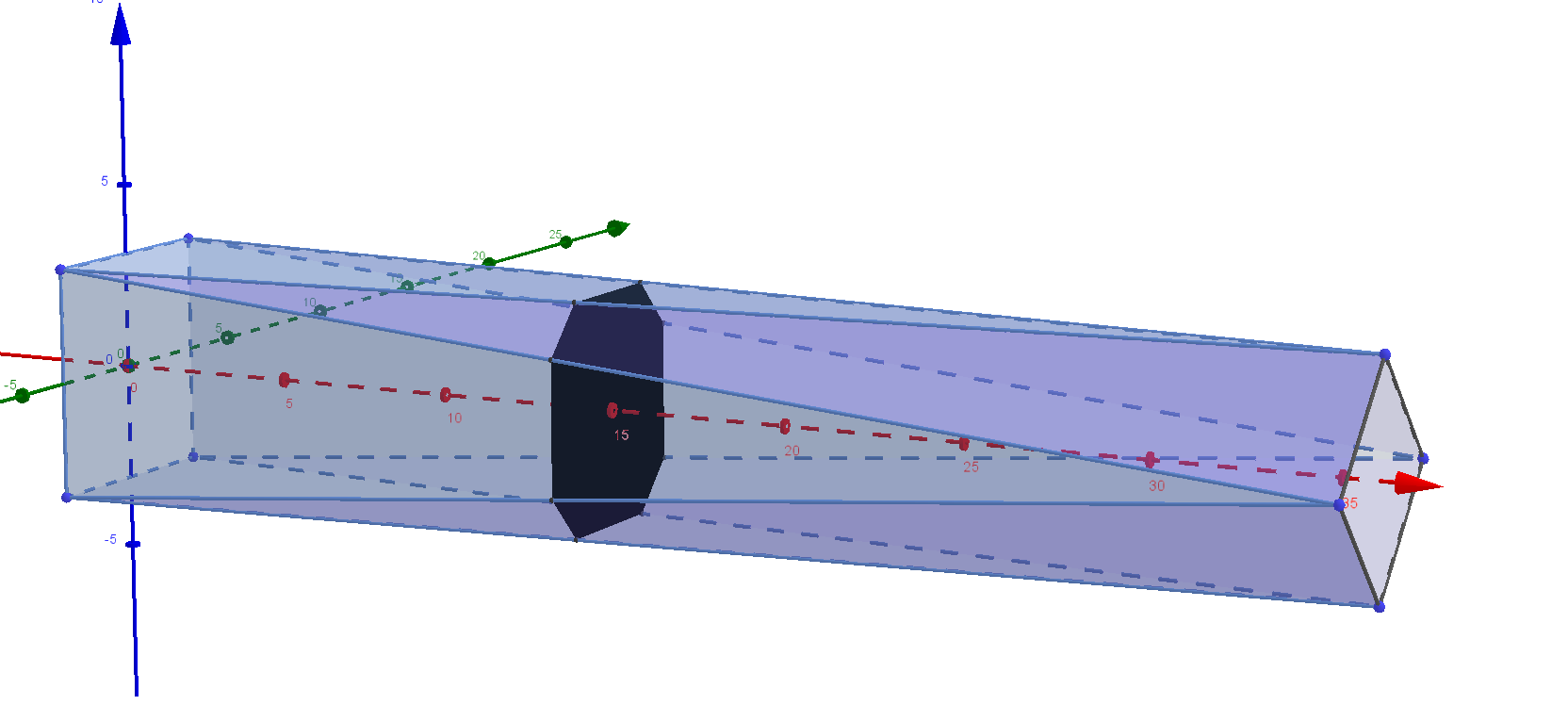
Das Volumen des Antiprismas kann wie bei Rotationskörpern durch ein Integral über die Querschnittsfläche berechnet werden.
Die Funktion für die Querschnittsfläche ist \[ f(x)=38,44 - 19,22\cdot \frac{x^2}{36^2} \] Das Volumen ergibt sich also durch \[\begin{align} &\int \limits_0^{36} \left(38,44 - 19,22\cdot \frac{x^2}{36^2}\right)dx\\ = &\left[ 38,44 \cdot x -19,22 \cdot \frac{1}{3}\cdot \frac{x^3}{36^2} \right]_0^{36}\\ = &\left( 38,44 \cdot 36 -19,22 \cdot \frac{1}{3}\cdot \frac{36^3}{36^2} \right)\\ &\quad - \left( 38,44 \cdot 0 -19,22 \cdot \frac{1}{3}\cdot \frac{0^3}{36^2} \right)\\ = &\left( 38,44 \cdot 36 -19,22 \cdot \frac{1}{3}\cdot 36 \right)\\ &\quad - 0 \\ = &1153,2 \end{align}\] Das Volumen stimmt mit dem in der Aufgabe aus der Analytischen Geometrie überein.