Lösungshinweise Aufgabe 13 d
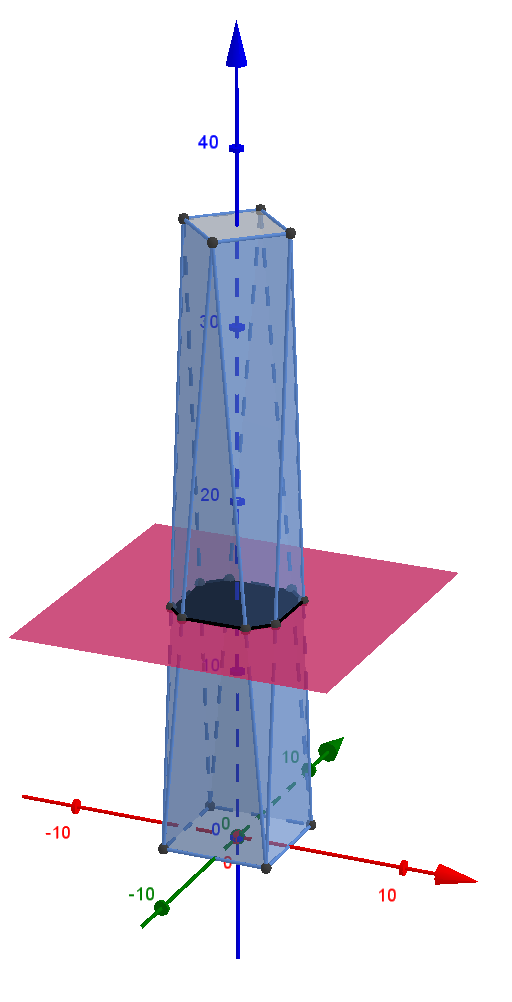
\[
f(x)=38,44 - 19,22\cdot \frac{x^2}{36^2}
\]
Um eine Extremstelle zu berechnen wird die erste Ableitung gleich 0 gesetzt.
\[
f'(x)=0 - 19,22\cdot \frac{2 x}{36^2}
\]
Ohne weiter umzuformen kann man bereits erkennen, dass die Ableitung
nur für x = 0 zu 0 wird.
Die einzige mögliche Extremstelle liegt also bei x = 0.
Da
\[
f''(x)=-19,22\cdot \frac{2 }{36^2}
\]
stets kleiner als 0 ist, liegt bei x = 0
ein Hochpunkt vor.
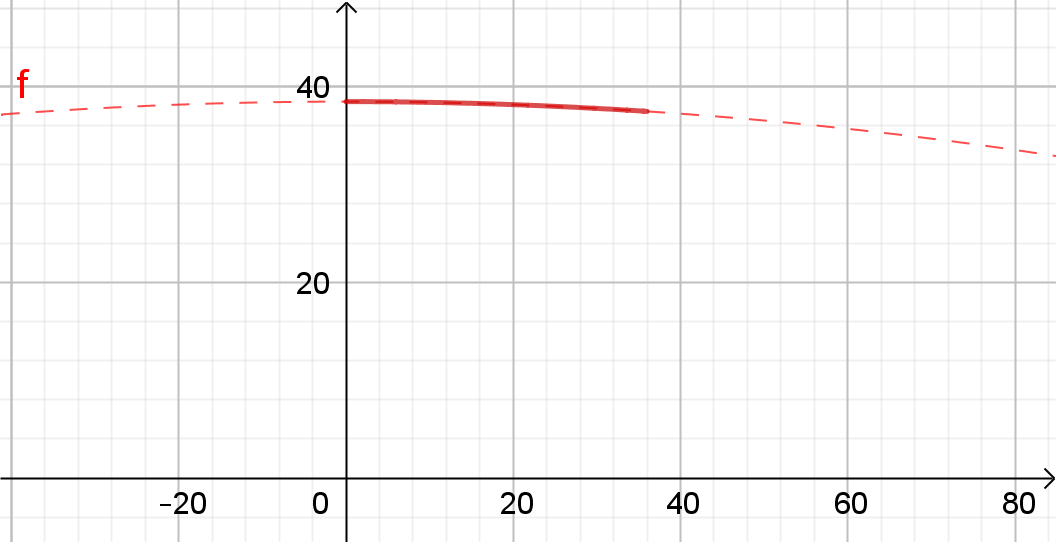
Der Funktionsgraph ist eine Parabel mit dem Scheitelpunkt
S=( 0 | 38,44 )
Nur der Bereich 0 ≤ x ≤ 36
kann für das Antiprisma verwendet werden.