Lösungshinweise Aufgabe 13 c
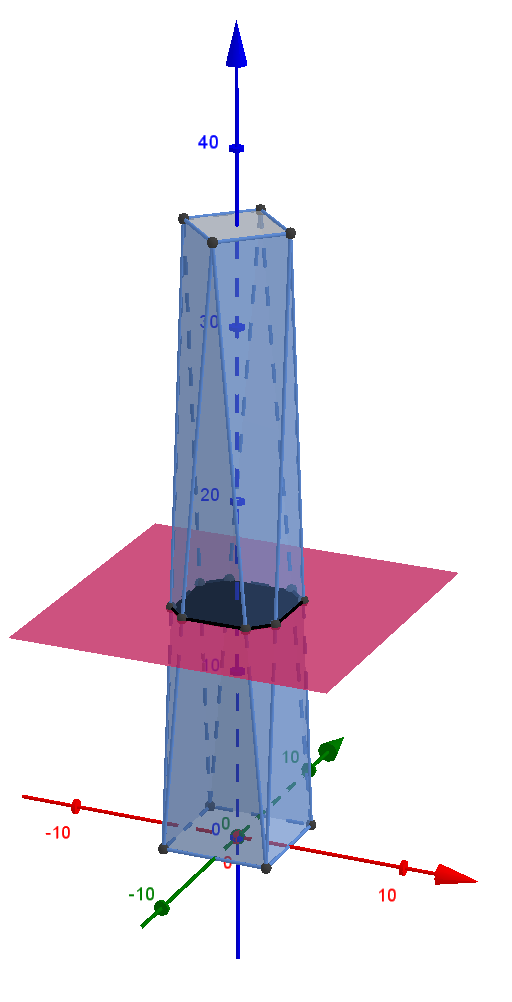
Für die Querschnittsfläche in der Höhe x ist
die Formel gegeben:
\[
f(x)=38,44 - 19,22\cdot \left(\frac{x}{36} \right)^2
\]
Für f (x)
setzt man den Mittelwert 28,83
ein, vgl. Aufgabenteil b):
\[\begin{align}
28,83&=38,44 - 19,22\cdot \left(\frac{x}{36} \right)^2 &\Leftrightarrow \\
28,83-38,44 &= - 19,22\cdot \left(\frac{x}{36} \right)^2 &\Leftrightarrow \\
-9,61 &= - 19,22\cdot \left(\frac{x}{36} \right)^2 &\Leftrightarrow \\
\frac{1}{2} &= \left(\frac{x}{36} \right)^2 &\Leftrightarrow \\
\frac{x}{36} &= \sqrt{\frac{1}{2}} &\Leftrightarrow \\
x &= 36 \cdot\sqrt{\frac{1}{2}} &\Leftrightarrow \\
x &\approx 36 \cdot 0,7071 &\Leftrightarrow \\
x &\approx 25,5
\end{align}\]
Der Mittelwert von Grund- und Dachfläche wird also nicht bei der Hälfte
der Gesamthöhe, sondern ungefähr beim 0,7-fachen der Gesamthöhe erreicht.