Lösungshinweise Aufgabe 12 c
\(
\begin{align}
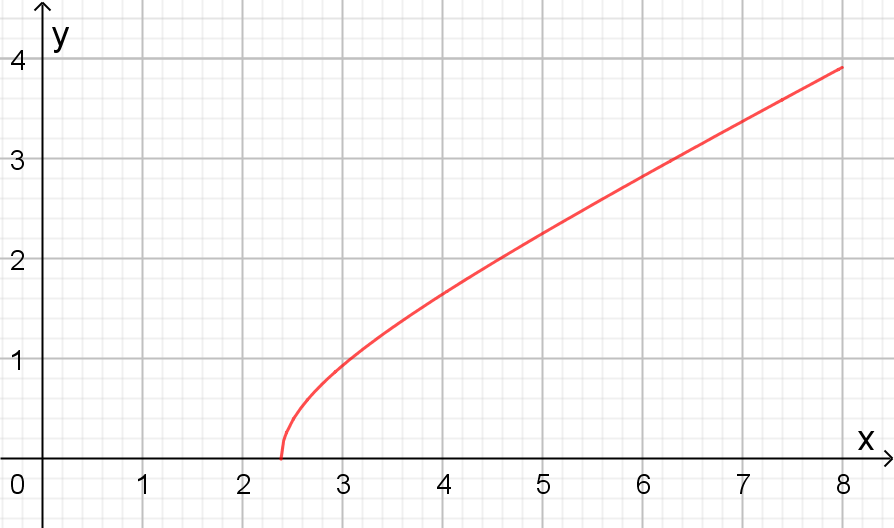
g(x) = \sqrt{\left(\frac{x}{1,95}\right)^2 - 1,5} \\
\end{align}
\)
Es ist die Nullstelle gesucht, also wird der Funktionsterm gleich 0 gesetzt:
\(
\begin{align}
&\sqrt{\left(\frac{x}{1,95}\right)^2 - 1,5} &&\negthickspace\negthickspace\negthickspace= 0 \\
&\Leftrightarrow \left(\frac{x}{1,95}\right)^2 - 1,5 &&\negthickspace\negthickspace\negthickspace= 0 \\
&\Leftrightarrow \left(\frac{x}{1,95}\right)^2 &&\negthickspace\negthickspace\negthickspace= 1,5 \\
&\Leftrightarrow \frac{x}{1,95} &&\negthickspace\negthickspace\negthickspace= \sqrt{1,5} \\
&\Leftrightarrow \qquad x &&\negthickspace\negthickspace\negthickspace= 1,95\cdot\sqrt{1,5} \\
&\Leftrightarrow \qquad x &&\negthickspace\negthickspace\negthickspace\approx 2,39 \\
\end{align}
\)
Dieser Wert stimmt gut mit der Nullstelle Graphen in der Abbildung überein.