Lösungshinweise Aufgabe 12 b
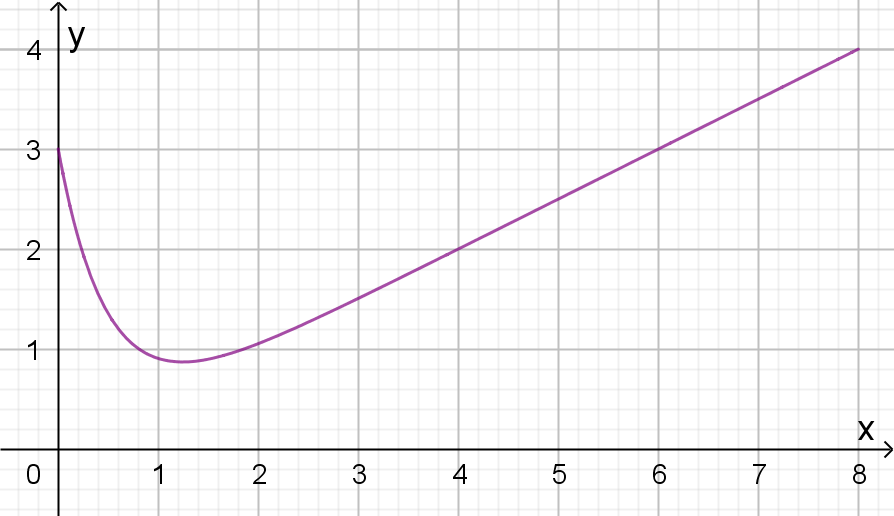
Notwendige Bedingung für einen Wendepunkt ist, dass die zweite Ableitung 0 ist. Aus
\(
\begin{align}
f(x) &= 3 \cdot e^{-2 x} + 0,5 x \\
f'(x) &= -6 \cdot e^{-2 x} + 0,5 \\
f''(x) &= +12 \cdot e^{-2 x}
\end{align}
\)
folgt, dass die zweite Ableitung stets positiv ist:
e-2x ist stets positiv.
Somit kann es keinen Wendepunkt geben.
Da die zweite Ableitung überall positiv ist, ist der Graph überall links gekrümmt und ändert an keiner Stelle die Krümmungsrichtung.