Hinweise zu Aufgabe 9, Teil g
Die bis zum Zeitpunkt x aufgenommene Wirkstoffmenge entspricht
dem Integral von 0 bis x über die Funktion f,
veranschaulicht durch den Inhalt der blau eingefärbten Fläche.
Im GeoGebra-Applet ist der Punkt G beim Zeitpunkt x eingetragen,
wobei seine y-Koordinate
dem Wert des Flächeninhalts (also der aufgenommenen Wirkstoffmenge)
entspricht.
Mit dem Schieberegler können Sie den Zeitpunkt x verändern.
Die Spur des Punktes G beschreibt den Graphen der Funktion G(x).
Da f(x) die aufgenommene Wirkstoffmenge pro Minute angibt und G(x) die bis zum Zeitpunkt x insgesamt aufgenommene Wirkstoffmenge, haben f und G verschiedene Maßeinheiten und Maßstäbe.
Das Integral hat jetzt die obere Grenze
x.
Deshalb kann die Variable im Integral nicht dieselbe Bezeichnung haben.
Meistens ersetzt man sie durch
t.
Man schreibt also:
\(
G(x)
=
\int\limits_0^x{f(t)}\mathrm{d}t
\) oder
\[
\begin{align}
G(x) &=
\int \limits_0^{x}{10\cdot e^{-0.005 t}}\mathrm{d}t
=
\left[
-2000\cdot e^{-0.005 t}
\right]_0^x\\
&=
-2000\cdot e^{-0.005 \cdot x}
-(-2000\cdot e^{-0.005 \cdot 0})\\
&=
-2000\cdot e^{-0.005 \cdot x}
+2000\\
&=
\text{ } 2000 \cdot(1-e^{-0.005 \cdot x})
\end{align}
\]
Die Funktion G(x) ist wie die in den vorigen Aufgabenteilen bereits
verwendete Funktion F(x) eine Stammfunktion zu f(x).
Bei beiden ist also die Ableitung f(x), an jeder Stelle x ist also
die Steigung von F gleich der von G.
Der Graph von G geht durch Verschiebung um
2000 Einheiten nach oben aus dem Graphen von F hervor.
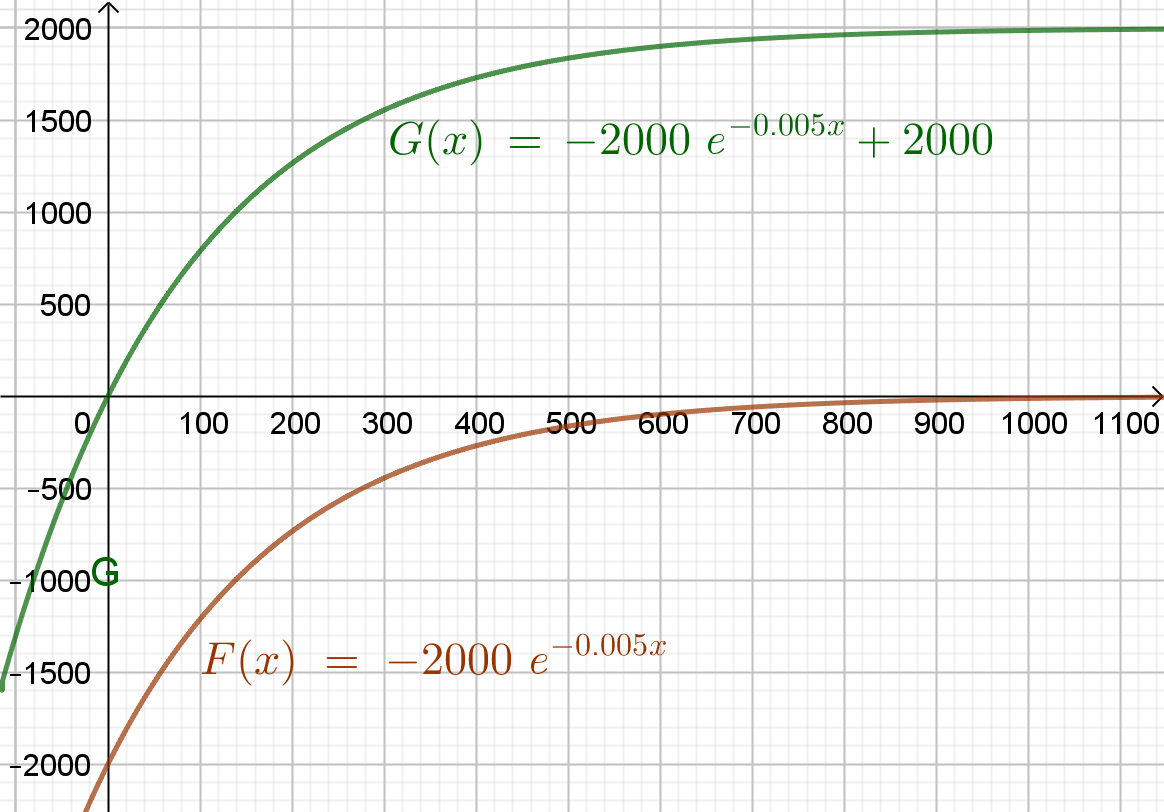
Der Funktionsterm und der Graph von G(x) lassen erkennen, dass für x→∞ der Grenzwert für die aufgenommene Wirkstoffmenge 2000μg beträgt.
Die Funktion \[ G(x) = \int \limits_0^{x}{10\cdot e^{-0.005 t}}\mathrm{d}t \] heißt Integralfunktion zu f(x), da sie durch ein Integral über die Funktion f definiert ist.