Hinweise zu Aufgabe 9, Teil f
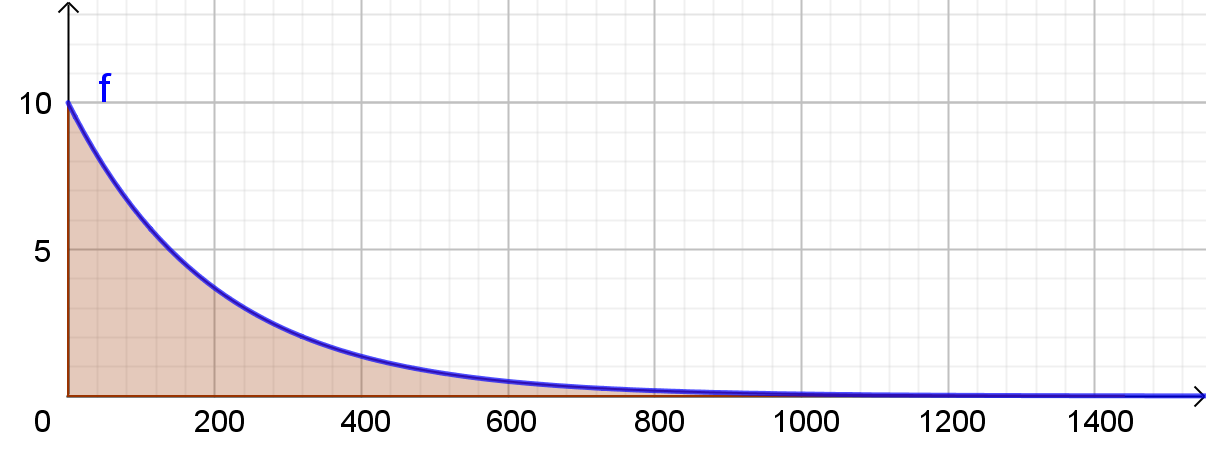
Die bis zum Zeitpunkt
b
aufgenommene Wirkstoffmenge wird wie
schon im vorigen Aufgabenteil durch ein Integral berechnet:
\(
\begin {align}
\int \limits_{0}^{b}{10 \cdot e^{-0,005 x}} \ \mathrm{d}x
&=
\left[
-2000 \cdot e^{-0,005 x}
\right]_0^{b}\\
&=
-2000 \cdot e^{-0,005 \cdot b}
-
(-2000 \cdot e^{-0,005 \cdot 0})\\
&=
-2000 \cdot e^{-0,005 \cdot b} - (-2000 \cdot e^{0})\\
&=
+ 2000 - 2000 \cdot e^{-0,005 \cdot b}
\end{align}
\)
Für
b
→ ∞
geht \(e^{-0,005 \cdot b} \rightarrow 0\).
Je größer
b
ist, desto weniger wird von +2000 abgezogen.
Die nach rechts offene, unbegrenzte Fläche wird also nicht unendlich groß.
Der Grenzwert des Flächeninhalts für
b → ∞
ist also 2000.
Man schreibt statt \[ \lim_{b \rightarrow \infty} \int \limits_{0}^{b} {10 \cdot e^{-0,005 x}} \ \mathrm{d}x = 2000 \] auch \[ \int \limits_{0}^{\infty} {10 \cdot e^{-0,005 x}} \ \mathrm{d}x = 2000 \] und bezeichent ein solches Integral als uneigentliches Integral, weil als obere Grenze keine reelle Zahl angegeben ist.