Hinweise zu Aufgabe 9, Teil e
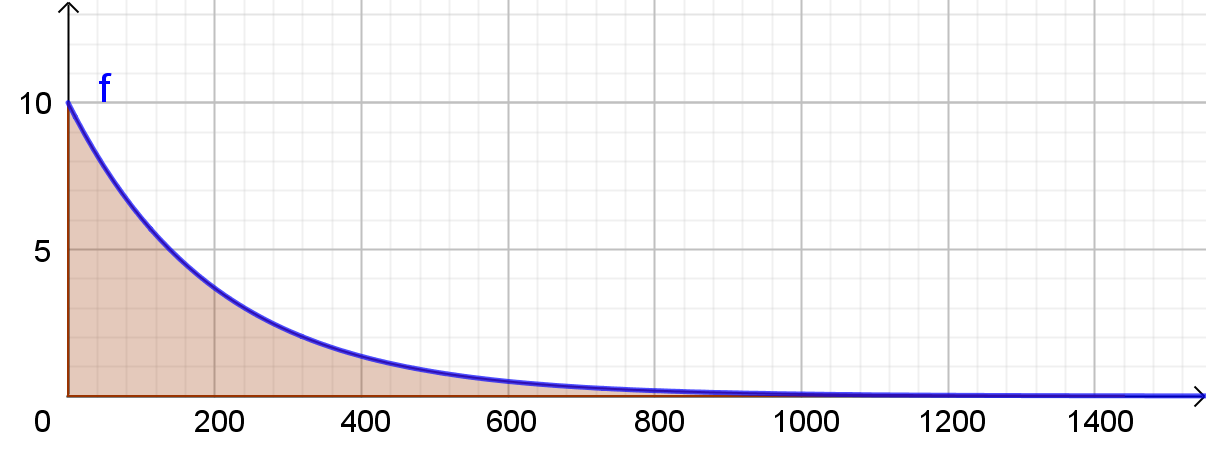
Nach 24h oder einem Tag wird fast kein Wirkstoff mehr aufgenommen:
Die monentane Wirkstoffaufnahme nach 24h = 1440min wäre
\(
f(1440)=10 \cdot e^{-0,005 \cdot 1440}
\approx 0,0075
\),
also
0,0075 μg min.
Die bis zu diesem Zeitpunkt aufgenommene Wirkstoffmenge wird wie
schon im vorigen Aufgabenteil durch ein Integral berechnet:
\(
\int \limits_{0}^{14400}{10 \cdot e^{-0,005 x}} \ \mathrm{d}x
\)
Mit der Stammfunktion
\(
F(x)=-2000 \cdot e^{-0,005 x}
\) ergibt sich
\(
\begin {align}
&\int \limits_{0}^{14400}{10 \cdot e^{-0,005 x}} \ \mathrm{d}x
=
\left[
-2000 \cdot e^{-0,005 x}
\right]_0^{1440}\\
&=
-2000 \cdot e^{-0,005 \cdot 1440}
-
(-2000 \cdot e^{-0,005 \cdot 0})\\
&=
-2000 \cdot e^{-7,2} - (-2000 \cdot e^{0})\\
&\approx
-1,49 + 2000
\end{align}
\)
Nach 24h sind also fast 2000μg aufgenommen worden.