Hinweise zu Aufgabe 9, Teil d
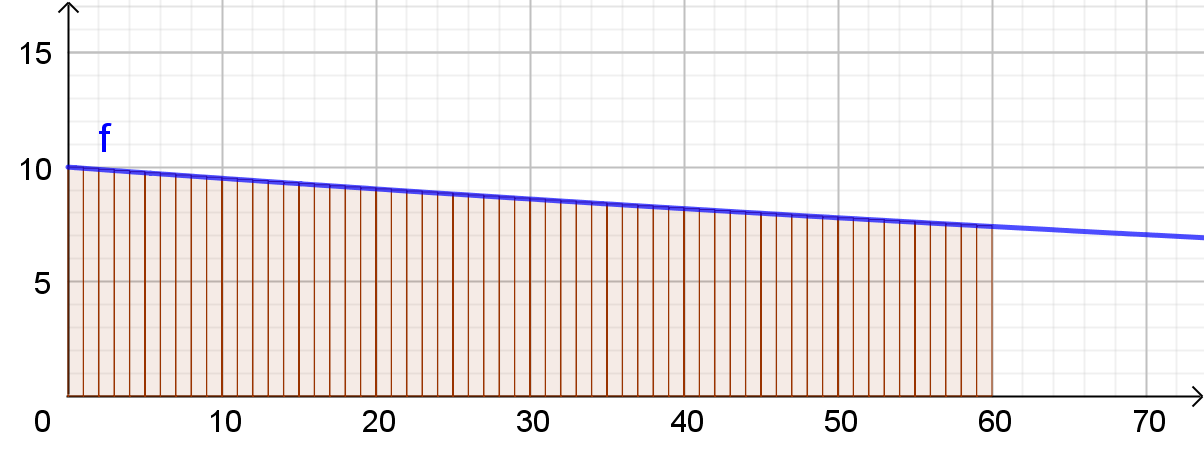
Wenn zu Beginn die Geschwindigkeit der Wirkstoffaufnahme
10 μg min
beträgt, und wir diesen Wert mit der Zeit 1min multiplizieren, erhalten wir die
Wirkstoffmenge in μg, die in der ersten Minute aufgenommen wird.
In der nächsten Minute ist die Aufnahme gemäß der Funktion nur minimal geringer,
und auch für diese Minute muss die Geschwindigkeit der Wirkstoffaufnahme
mit der Zeit 1 Minute multipliziert werden.
Man könnte die 60 Minuten auch feiner aufteilen, z.B. in Sekunden — letztenendes zeigt sich, dass die insgesamt aufgenommene Wirkstoffmenge statt durch eine Summe mit 60 Summanden (oder mehr, bei feinerer Aufteilung) besser mit einem Integral berechnet werden kann.
Es ist also folgendes Integral zu berechnen: \[ \int \limits_{0}^{60}{10 \cdot e^{-0,005 x}}\mathrm{d}x \]
Eine Stammfunktion zu \( f(x)=10 \cdot e^{-0,005 x} \) ist \( F(x)=-2000 \cdot e^{-0,005 x} \). Sie können das leicht durch Ableiten dieser Stammfunktion bestätigen, dabei ist die Kettenregel (vgl. Arbeitsblatt 5) zu beachten.
Also:
\(
\int \limits_{0}^{60}{10 \cdot e^{-0,005 x}}\mathrm{d}x
=
\left[
-2000 \cdot e^{-0,005 x}
\right]_{0}^{60} =
\) …