Lösungshinweise Aufgabe 3j
Es ist
\(
f(x)=-\frac{1}{1280}x^5 + \frac{1}{40}x^4 - \frac{21}{80}x^3 + \frac{9}{10}x^2
\)
oder
\(
v(t)=-\frac{1}{1280}t^5 + \frac{1}{40}t^4 - \frac{21}{80}t^3 + \frac{9}{10}t^2
\)
Dann sind dazu passende Stammfunktionen
\(
F(x)=-\frac{1}{1280}\cdot\frac{1}{6}x^6 + \frac{1}{40}\cdot\frac{1}{5}x^5 - \frac{21}{80}\cdot\frac{1}{4}x^4 + \frac{9}{10}\cdot\frac{1}{3}x^3
\),
also
\(
F(x)=-\frac{1}{7680}x^6 + \frac{1}{200}x^5 - \frac{21}{320}x^4 + \frac{3}{10}x^3
\)
oder
\(
s(t)=-\frac{1}{7680}t^6 + \frac{1}{200}t^5 - \frac{21}{320}t^4 + \frac{3}{10}t^3
\)
Damit lässt sich der Ort (die Höhe) der Drohne berechnen:
Zum Zeitpunkt t=0 beträgt die Höhe
\( s(0) = 0 \).
Nach 8 Sekunden beträgt ihre Höhe
\(
\begin{align}
s(8)&=-\frac{1}{7680}\cdot 8^6 + \frac{1}{200}\cdot 8^5 - \frac{21}{320}\cdot 8^4 + \frac{3}{10}\cdot 8^3 \\
&\approx 14,51
\end{align}
\)
Sie befindet sich dann also in ca. 14,51m Höhe.
Nach 12s beträgt ihre Höhe
\(
\begin{align}
s(12)&=-\frac{1}{7680}\cdot 12^6 + \frac{1}{200}\cdot 12^5 - \frac{21}{320}\cdot 12^4 + \frac{3}{10}\cdot 12^3 \\
&= 12,96
\end{align}
\)
In der Zeit von 8s bis 12s ist sie also um ca. 1,55m gesunken.
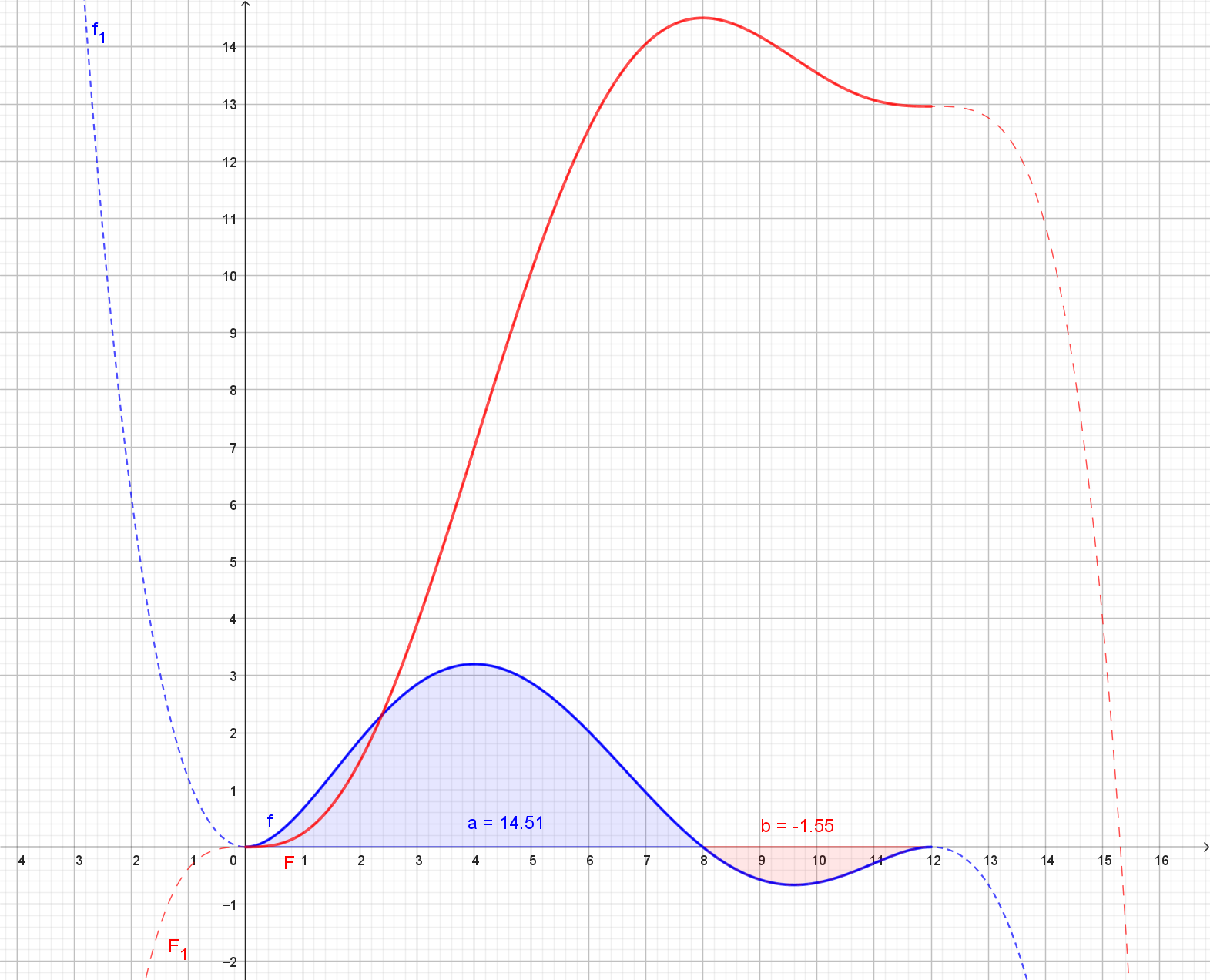
Es folgen die Graphen für v(t) und s(t) in einem gemeinsamten Koordinatendiagramm.
Zu beachten ist, dass die Werte an der y-Achse einerseits für die Geschwindigkeit in m/s stehen
und andererseits auch für die Höhe der Drohne in m.