Lösungshinweise Aufgabe 1c

Zeichnen mit GeoGebra

Verwenden Sie gern wieder GeoGebra zum Zeichnen des Orts-Zeit-Diagramms, wenden Sie die Tipps zum Zeichnen aus den Hinweisen zum Aufgabenteil 1a an.

Zeichnen einzelner Punkte

Falls Sie noch nicht wissen, mit welcher Funktion Sie den Graphen für den Ort des Radfahrers darstellen können, überlegen Sie sich mit Hilfe der Ergebnisse von Aufgabenteil 1b ein paar Eckdaten:

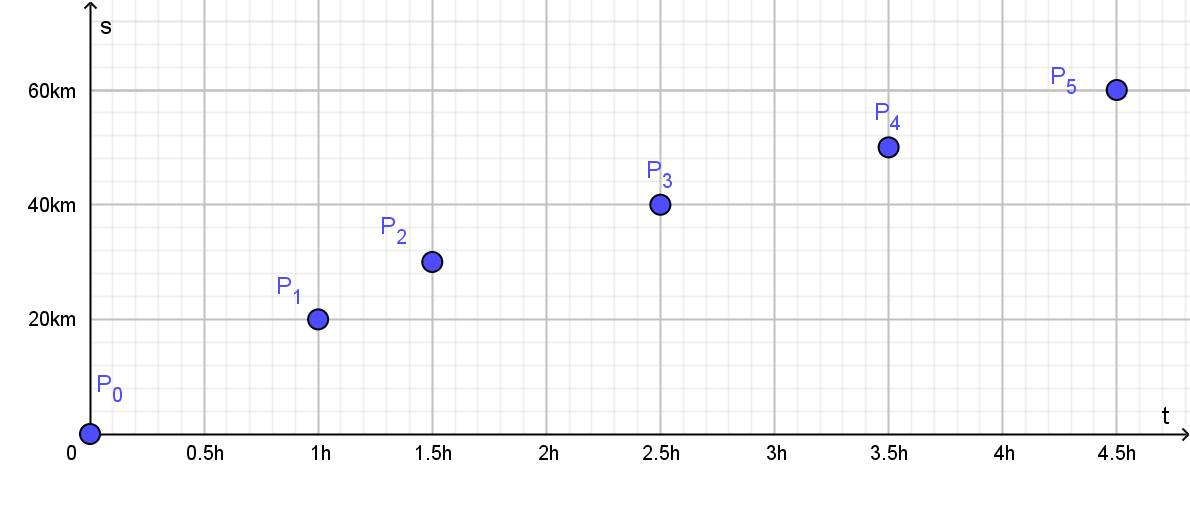
Wo befindet sich der Radfahrer zu den Zeitpunkten t = 0h, t = 1h, t = 1.5h, t = 2.5h, t = 3.5h, t = 4.5h?

Dadurch erhalten Sie die Punkte (0h | 0km), (1h | 20km), (1.5h | 30km), (2.5h | 40km), (3.5h | 50km), (4.5h | 60km).
Tragen Sie diese Punkte in das Koordinaten­dia­gramm ein, z.B. durch Eingaben wie
P_3 = (3.5, 50)

Zeichnen der Funktion(en)

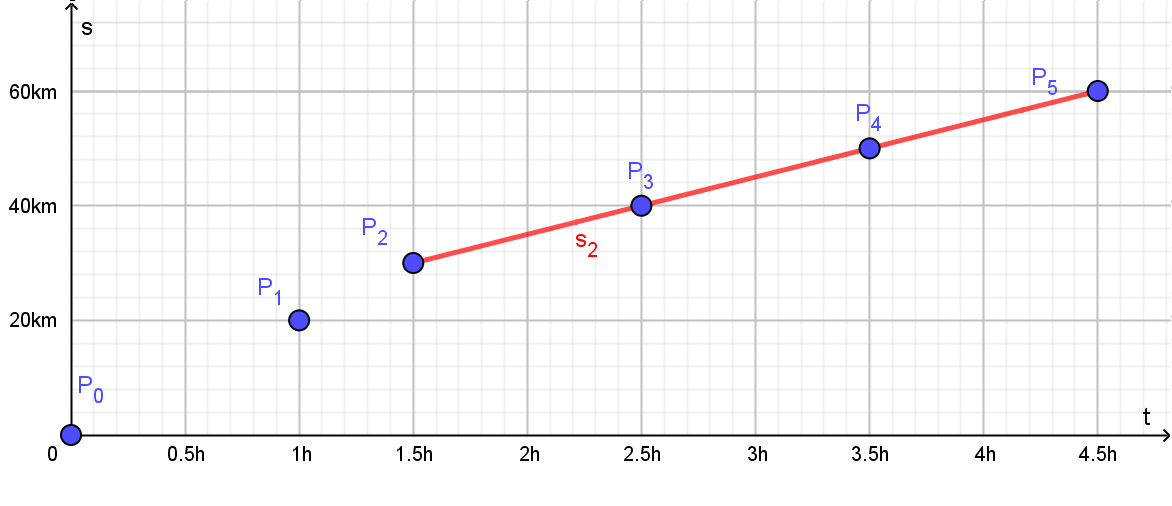
Zu Anfang beträgt die Geschwin­dig­keit des Radfahrers 20km/h. Der zurückgelegte Weg ist
Weg = Geschwindigkeit × Zeit, also
f(x) = 20 * x
oder
s_1(t) = 20 * t
oder mit Bereichsgrenzen (vgl. Hinweise zu Aufgabenteil 1a)
s_1(t) = 20 * t, (0 ≤ t ≤ 1.5)

Die zweite Funktion hat nur eine halb so große Steigung, und sie verläuft nicht durch den Koordinaten­ursprung. Überlegen Sie sich, um wie viele Einheiten sie noch nach oben verschoben werden muss, damit ihr Graph durch die Punkte P₂, P₃, P₄ und P₅ verläuft.

Zusammenhang zwischen \(v(t)\) und \(s(t)\)

Hier sind noch einmal die beiden Graphen für die Geschwindigkeit und für den Ort in einer Abbildung zusammen­gestellt:

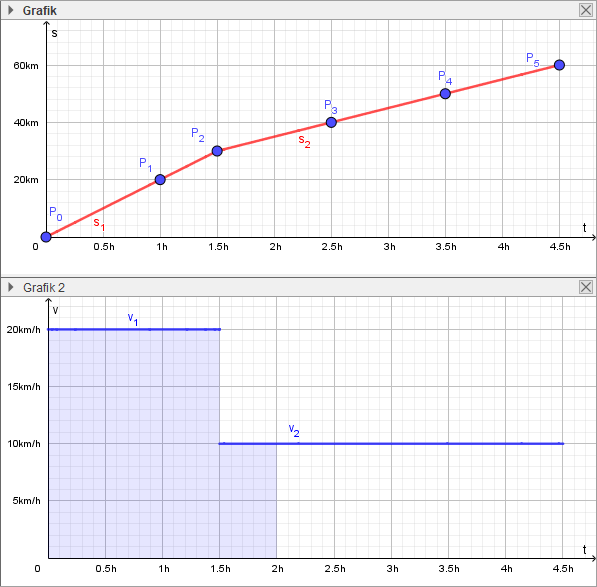
Für t = 1,5h ist der Ort 30km, und das entspricht genau der Fläche unter dem Graphen von t=0 bis t=1,5 im v‑t‑Diagramm.

Mathematisch entspricht der Ort dem sogenannten Integral über der Geschwin­dig­keits­funktion, dazu mehr in der nächsten Aufgabe.

Geht man von der Orts­funktion aus, so lässt sich feststellen, dass die Geschwin­dig­keits­funktion die Ableitung der Orts­funktion ist.

zurück zur Aufgabe