Lösungshinweise Aufgabe 31 g

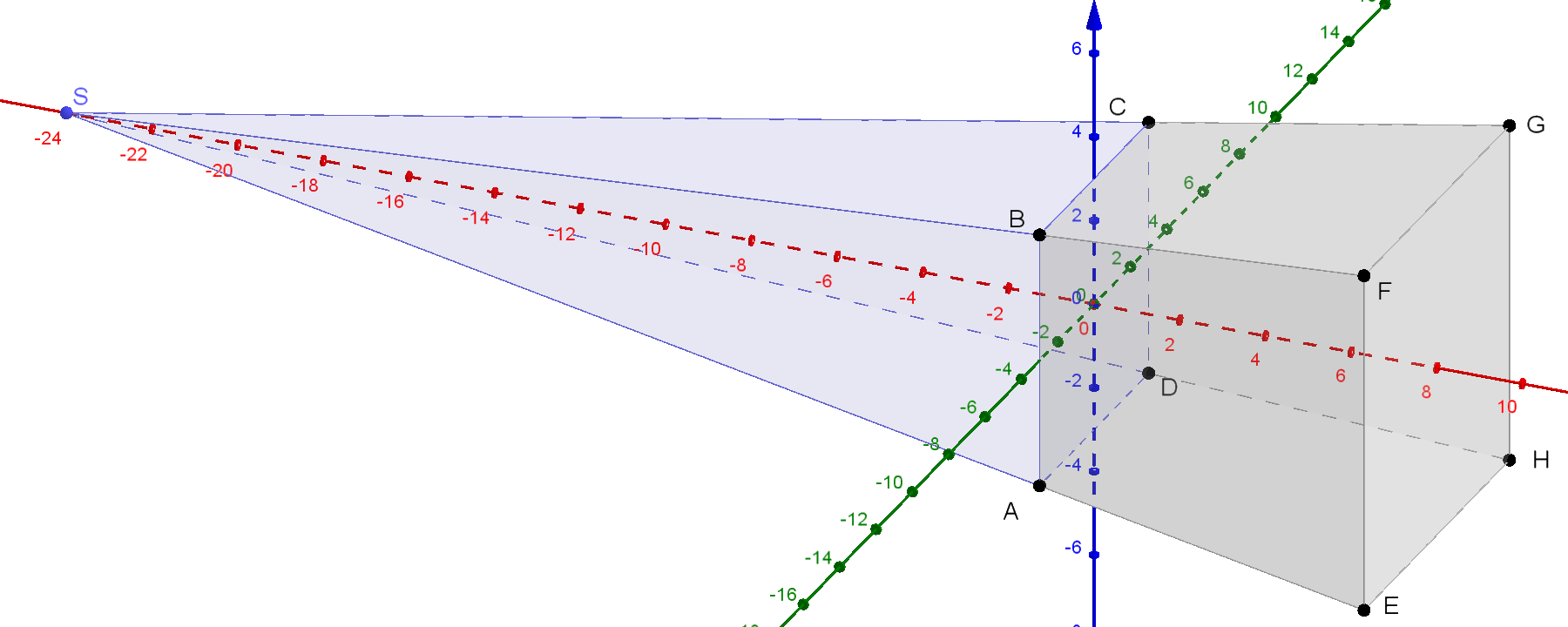
Um das Volumen des Pyramidenstumpfes zu berechnen, kann man den Stumpf zu einer ganzen Pyramide ergänzen.
Dazu muss man herausfinden, wo diese ihre Spitze S hat.
Aus Symmetriegründen muss S auf der x‑Achse liegen.

Es gibt verschiedene Möglichkeiten, um die x‑Koordinate von S zu finden.
Man könnte z.B. die Gerade aus Aufgabenteil c) betrachten und untersuchen, bei welchem Wert des Parameters r der x₂‑Wert 0 und der x₃‑Wert 0 wird.

Ich habe mir überlegt, dass wenn ich von Punkt F zu Punkt B gehe, ich mich um eine Einheit nach unten und um eine Einheit in Richtung der x₂‑Achse (grün) bewege. Und ich gehe dabei um 8 Einheiten in Richtung der negativen x₁‑Achse.
In Punkt B=(0|-3| 3) befinde ich mich noch um 3 Einheiten über der x₁x₂‑Ebene. Ich muss diesen Step also noch dreimal ausführen.
Dann befinde ich mich auf der x₁‑Achse an der Stelle -24.
S=(-24| 0| 0).

Die gesamte Pyramide hat als Grundfläche das Quadrat EFGH mit dem Flächeninhalt G₁ = 8×8 = 64 und das Volumen \[\begin{align} V_1 &= \frac{1}{3} \; G_1 \cdot h_1 \\ &= \frac{1}{3}\cdot 64 \cdot (8+24)\\ &= \frac{1}{3} \cdot 2048 \approx 682,7 \end{align}\]

Das Volumen der ergänzten Pyramide hat die Grundfläche ABCD mit dem Flächeninhalt G₂ = 6×6 = 36 und das Volumen \[\begin{align} V_2 &= \frac{1}{3} \; G_2 \cdot h_2 \\ &= \frac{1}{3}\cdot 36 \cdot 24\\ &= \frac{1}{3} \cdot 864 = 288 \end{align}\]

Das Volumen des Pyramidenstumpfes ist somit \(V_{\text{Pyramidenstumpf}} \approx 682,7 - 288 = 394,7\)

zurück zur Aufgabe