Lösungshinweise Aufgabe 31 g
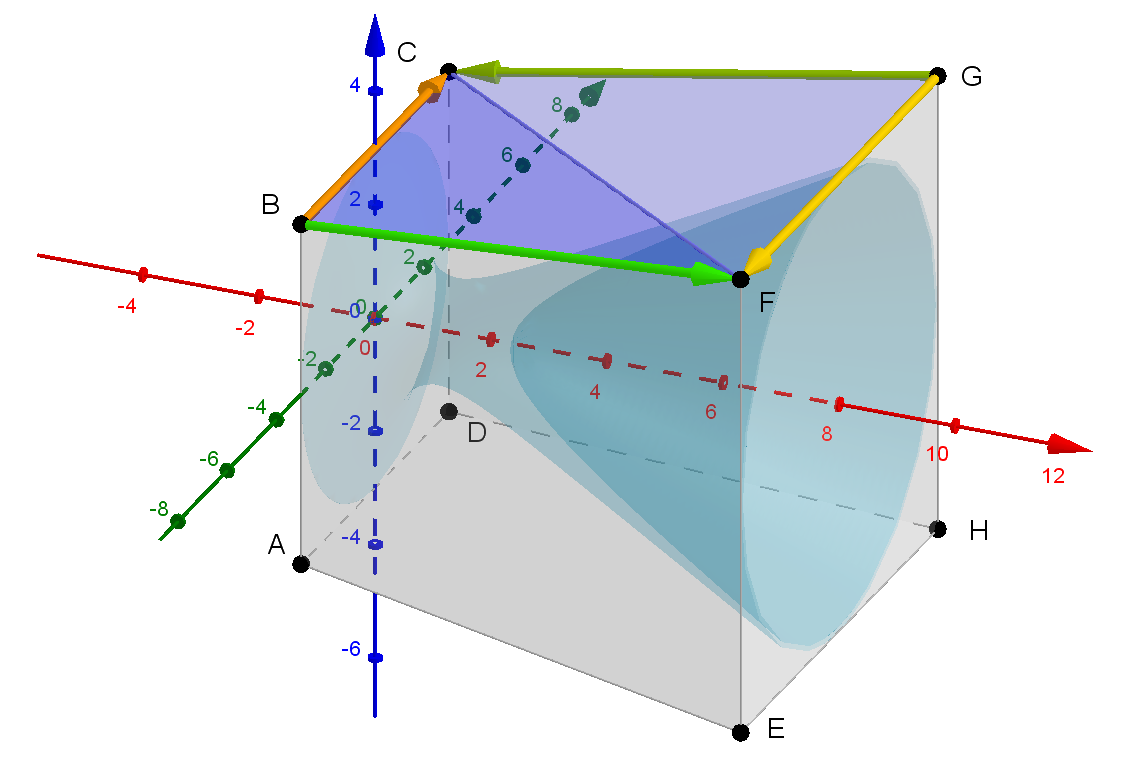
Das Trapez BFGC wird in zwei Teildreiecke zerlegt und für diese wird der Flächeninhalt berechnet. A1 sei der Flächeninhalt des Dreiecks BFC. \[\begin{align} A_1 &= \frac{1}{2}\cdot\vert\vec u \times \vec v \vert\\ &= \frac{1}{2}\cdot\vert\vec n\vert\\ &= \frac{1}{2}\cdot\left|\pmatrix{-6\\0\\48}\right|\\ &= \frac{1}{2}\cdot\sqrt{6^2 + 48^2}\\ &= \frac{1}{2}\cdot\sqrt{2340}=3\sqrt{65}\approx 24,2 \end{align}\] Der Normalenvektor wurde bereits im Aufgabenteil e) berechnet.
A2 sei der Flächeninhalt des
Dreiecks GCF.
Es wird von den Vektoren
\(\vec a = \overrightarrow{GC} \)
und
\(\vec b = \overrightarrow{GF} \)
aufgespannt. Es ist
\(\vec a = \overrightarrow{GC}=\pmatrix{-8\\-1\\-1}\)
und
\(\vec b = \overrightarrow{GF}=\pmatrix{0\\-8\\0}\).
Damit wird
\[\begin{align}
A_2
&=\frac{1}{2}\cdot\left|\pmatrix{-8\\-1\\-1} \times\pmatrix{0\\-8\\0}\right|\\
&=\frac{1}{2}\cdot\left|\pmatrix{-8\\0\\64}\right|\\
&=\frac{1}{2}\cdot\sqrt{8^2 + 0^2 + 64^2}\\
&=\frac{1}{2}\cdot\sqrt{4160}=4\sqrt{65}\approx 32,2
\end{align}\]
Der Flächeninhalt des Trapezes ist die Summe der beiden Flächeninhalte, also \[ A_{\text{Trapez}} = 3\sqrt{65} + 4\sqrt{65} = 7\sqrt{65} \approx \underline{\underline{56,4}} \]