Lösungshinweise Aufgabe 31 f
Die Ebene durch die Punkte B, A und F hat die Ebenengleichung
\[
E_{\,\small\text{BAF}}: \quad \vec x = \pmatrix{0\\-3\\3} \;+\; \lambda \cdot \pmatrix{0\\0\\-6} \;+\; \mu \cdot \pmatrix{8\\-1\\1} \;\lambda,\mu\in \mathbb{R}
\]
Dabei ist der erste Richtungvektor der bereits bekannte Vektor von B nach F, und der zweite
ist der Vektor von B nach A.
Einen Normalenvektor zu dieser Ebene erhält man wieder durch das
Vektorprodukt der beiden Richtungsvektoren:
\[
\vec n_{\,\small\text{BAF}} = \pmatrix{0\\0\\-6} \times \pmatrix{8\\-1\\1} = \pmatrix{-6\\-48\\0}
\]
Den Winkel zwischen den beiden Ebenen \(E_{\,\small\text{BFC}}\) und \(E_{\,\small\text{BAF}}\)
können wir ermitteln, indem wir zunächst den Winkel berechnen, den die beiden
zugehörigen Normalenvektoren bilden:
\(
\text{(I)}\qquad\vec n_{\,\small\text{BFC}} \cdot \vec n_{\,\small\text{BAF}} = \vert\vec n_{\,\small\text{BFC}}\vert\cdot\vert\vec n_{\,\small\text{BAF}}\vert\cdot\cos(\beta)
\)
Für beide Normalenvektoren ist der Betrag gleich, nämlich
\(\left|\vec n_{\,\small\text{BFC}}\right| = \left|\vec n_{\,\small\text{BAF}}\right| = \sqrt{6^2+48^2}=\sqrt{2340}=6\sqrt{65}\)
Eingesetzt in (I):
\[
\pmatrix{-6\\0\\48} \cdot \pmatrix{-6\\-48\\0} = 6\sqrt{65} \cdot 6\sqrt{65}\cdot \cos(\beta)
\]
\[
36 = 6 \cdot 6 \cdot \sqrt{65} \cdot \sqrt{65} \cdot \cos(\beta)
\]
\[
\cos(\beta) = \frac{1}{65}
\]
\[
\beta = \cos^{-1}\left(\frac{1}{65}\right)\approx 89,12°
\]
Achtung!
Normalerweise gibt man als Winkel zwischen zwei Ebenen den Winkel an, der
kleiner als 90° ist.
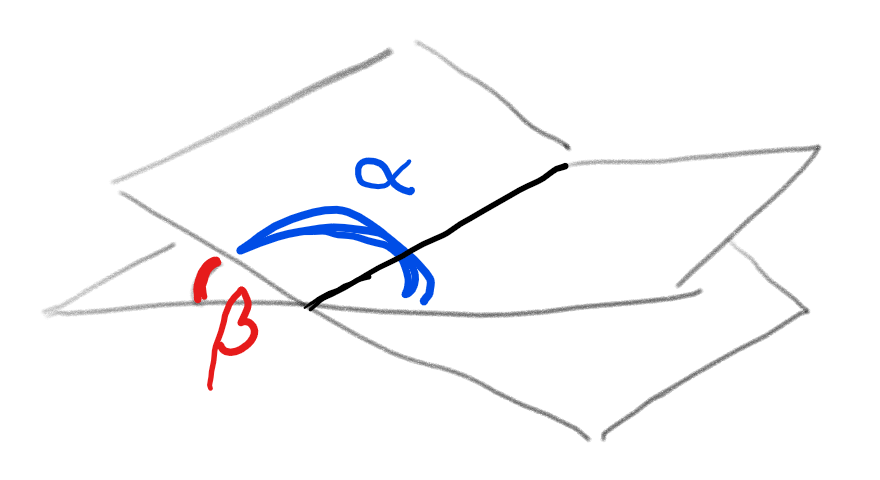
Hier ist aber der Winkel zwischen den beiden Flächenstücken des Kartons
gesucht, und dieser muss etwas größer als 90° sein.
Deshalb ist hier der größere Winkel α = 180° − β
als Winkel zwischen den beiden Seitenflächen des Pyramidenstumpfs anzugeben,
also \[\alpha \approx 180° - 89,12 = \underline{\underline{90,88°}} \]