Lösungshinweise Aufgabe 31 a
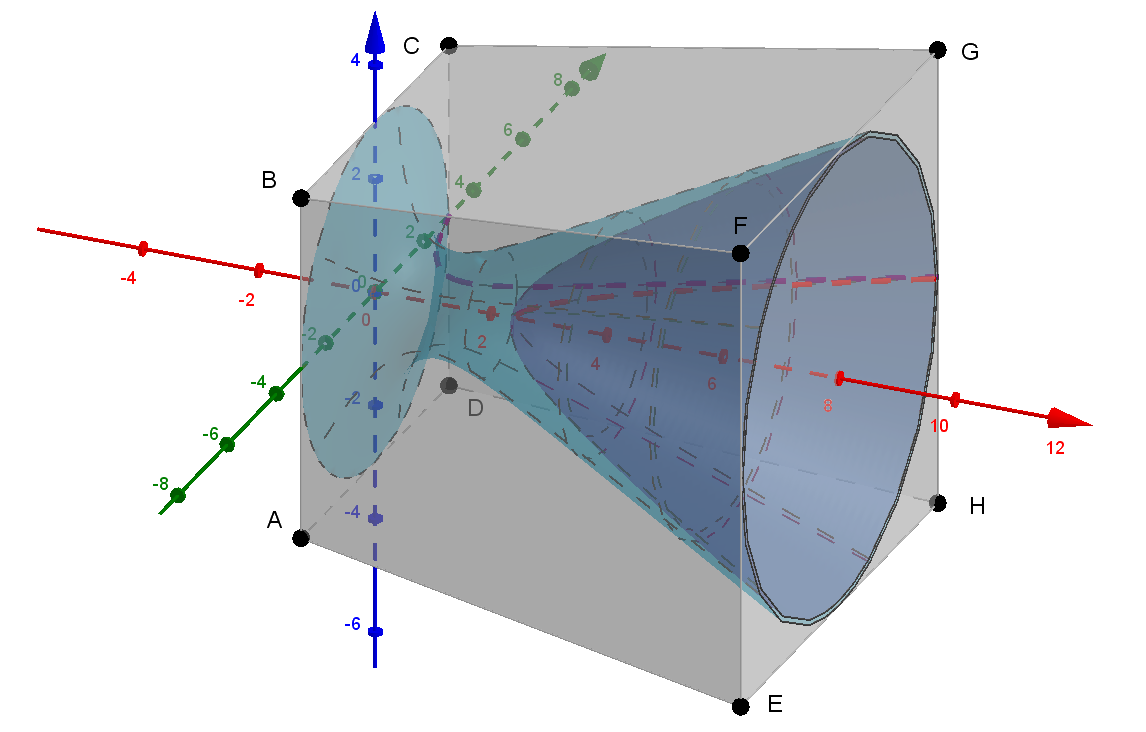
Die Eckpunkte des Kartons sind
A=(0,-3,-3), B=(0,-3, 3), C=(0, 3, 3), D=(0, 3,-3)),
E=(8,-4,-4), F=(8,-4, 4), G=(8, 4, 4), H=(8, 4,-4).
Von B nach F führt der Vektor \(\vec u = \overrightarrow{BF}=\pmatrix{8\\-1\\1}\).
Von B nach C führt der Vektor \(\vec v = \overrightarrow{BC}=\pmatrix{0\\6\\0}\).
Man kann die Koordinaten (manche sagen auch: Komponenten) dieser Vektoren
jeweils als Differenz der Koordinaten des End- und Anfangspunkts des Vektors
berechen.
Man erhält den Vektor aber auch anschaulich, wenn man sich z.B. für
\(\vec u = \overrightarrow{BF}\) fragt, wie die Beschreibung für den
Weg von B nach F lautet:
Gehe 8 Einheiten in
x‑Richtung (im Bild die rote Achse),
dann um −1 in y‑Richtung (grüne Achse, negative Richtung),
und schließlich noch um 1 Einheit nach oben in z‑Richtung
(blaue Achse)
.
Als Vektor geschrieben lautet diese Wegbeschreibung dann
\(\vec u=\pmatrix{8\\-1\\1}\)
Die Länge des Vektors
u→
ist
\(|\vec u| = \sqrt{8^2 + 1^2 + 1^2} = \sqrt{66} \approx 8,124\)
Die Länge des Vektors
v→
könnte man auf die gleiche Weise berechnen −
aber da er nur um 6 Einheiten in y‑Richtung
führt, kann man seine Länge auch ohne Berechnung
sofort mit \(|\vec v| = 6\,\) angeben.