Lösungshinweise Aufgabe 22 (II)

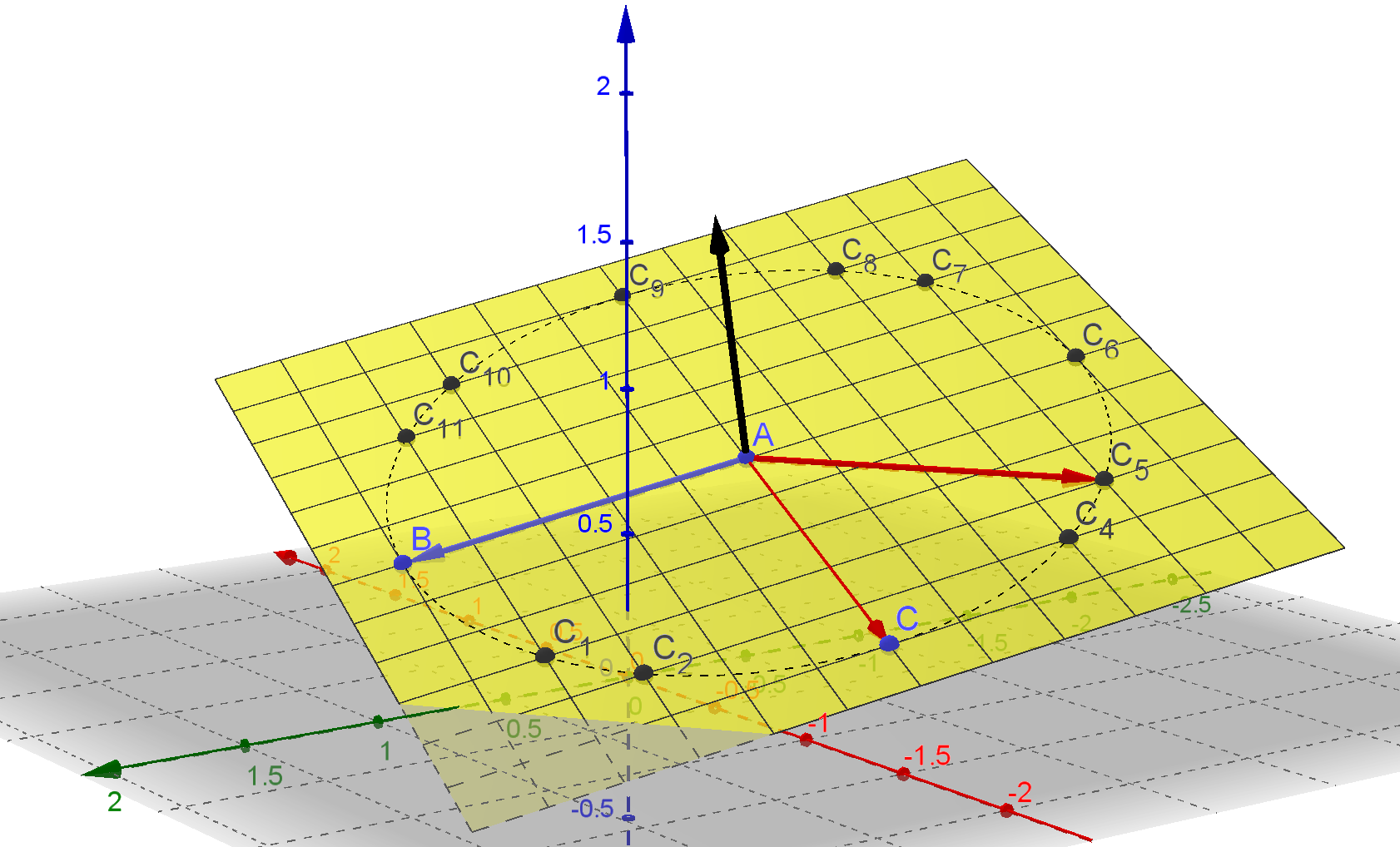
C₀ = B und C₃ = C waren gegeben.
Die Berechnung von C₁ und C₂ erfolgte im Aufgabenteil c. Entsprechend können die weiteren Punkte C₄ bis C₁₁ berechnet werden.
Man erhält:
C₀ = ( 0,8  |  0,4  | 0,30)
C₁ = ( 0    |  0,34 | 0,12)
C₂ = (−0,32 |  0,16 | 0,1 )
C₃ = (−0,8  |−0,50 | 0,2 )
C₄ = (−0,8  |−1,28 | 0,46)
C₅ = (−0,64 |−1,58 | 0,6 )
C₆ = ( 0    |−2,00 | 0,9 )
C₇ = ( 0,8  |−1,94 | 1,08)
C₈ = ( 1,12 |−1,76 | 1,1 )
C₉ = ( 1,6  |−1,1  | 1   )
C₁₀=( 1,6  |−0,32 | 0,74)
C₁₁=( 1,44 |−0,02 | 0,6 )

Die Vektoren, die von A = (0,4|−0,8|0,6) aus zu diesen Punkten führen, sind
\(\vec{v}_0 = \small{\begin{pmatrix}0,4\\1,2\\-0,3\end{pmatrix}}\), \(\vec{v}_1 = \small{\begin{pmatrix}-0,4\\1,14\\-0,48\end{pmatrix}}\), \(\vec{v}_2 = \small{\begin{pmatrix}-0,72\\0,96\\-0,5\end{pmatrix}}\),
\(\vec{v}_3 = \small{\begin{pmatrix}-1,2\\0,3\\-0,4\end{pmatrix}}\), \(\vec{v}_4 = \small{\begin{pmatrix}-1,2\\-0,48\\-0,14\end{pmatrix}}\), \(\vec{v}_5 = \small{\begin{pmatrix}-1,04\\-0,78\\0\end{pmatrix}}\),
\(\vec{v}_6 = \small{\begin{pmatrix}-0,4\\-1,2\\0,3\end{pmatrix}}\), \(\vec{v}_7 = \small{\begin{pmatrix}0,4\\-1,14\\0,48\end{pmatrix}}\), \(\vec{v}_8 = \small{\begin{pmatrix}0,72\\-0,96\\0,5\end{pmatrix}}\), …

Damit ergeben sich z.B. folgende Vektorprodukte:

\[ \begin{aligned} \vec{u} \times \vec{v}_3 & = \small{ \begin{pmatrix} 0,4 \\ 1,2 \\ -0,3 \end{pmatrix} \times \begin{pmatrix} -1,2 \\ 0,3 \\ -0,4 \end{pmatrix} } \\ \\ \vec{u} \times \vec{v}_3 & = \small{ \left( \begin{array}{rcr} 1,2 \cdot(-0,4) & - & (-0,3)\cdot 0,3 \\ -0,4\cdot(-0,4) & + & (-0,3)\cdot(-1,2) \\ 0,4\cdot 0,3 & - & 1,2\cdot(-1,2) \end{array} \right) } \\ \\ \vec{u} \times \vec{v}_3 & = \small{ \begin{pmatrix} -0,39 \\ 0,52 \\ 1,56 \end{pmatrix} } \end{aligned} \]

Zur Berechnung können Sie natürlich auch das Schema aus der Hilfe zur vorigen Aufgabe verwenden. Aus Platzgründen wurde hier darauf verzichtet.
Das nächste Vektorprodukt berechnen Sie ebenso:

\[ \begin{aligned} \vec{u} \times \vec{v}_4 & = \small{ \begin{pmatrix} 0,4 \\ 1,2 \\ -0,3 \end{pmatrix} \times \begin{pmatrix} -1,2 \\ -0,48 \\ -0,14 \end{pmatrix} } \\ \\ \vec{u} \times \vec{v}_4 & = \small{ \left( \begin{array}{rcr} 1,2 \cdot(-0,14) & - & (-0,3)\cdot(-0,48) \\ -0,4\cdot(-0,14) & + & (-0,3)\cdot(-1,2) \\ 0,4\cdot(-0,48) & - & 1,2\cdot(-1,2) \end{array} \right) } \\ \\ \vec{u} \times \vec{v}_4 & = \small{ \begin{pmatrix} -0,312 \\ 0,416 \\ 1,248 \end{pmatrix} } \end{aligned} \]

Vergleicht man diese ersten beiden Vektorprodukte, so stellt man fest, dass beide Ergebnisvektoren die gleiche Richtung haben:
Das zweite Ergebnis ist das 0,8-fache des ersten.

Das nächste Vektorprodukt berechnen Sie wieder auf die gleiche Weise:

\[ \begin{aligned} \vec{u} \times \vec{v}_5 & = \small{ \begin{pmatrix} 0,4 \\ 1,2 \\ -0,3 \end{pmatrix} \times \begin{pmatrix} -1,04 \\ -0,78 \\ 0 \end{pmatrix} } \\ \\ \vec{u} \times \vec{v}_5 & = \small{ \left( \begin{array}{rcr} 1,2 \cdot 0 & - & (-0,3)\cdot(-0,78) \\ -0,4\cdot 0 & + & (-0,3)\cdot(-1,04) \\ 0,4\cdot(-0,78) & - & 1,2\cdot(-1,04) \end{array} \right) } \\ \\ \vec{u} \times \vec{v}_5 & = \small{ \begin{pmatrix} -0,234 \\ 0,312 \\ 0,936 \end{pmatrix} } \end{aligned} \]

Der dritte Ergebnisvektor ist genau das 0,6-fache des ersten.
Er zeigt also wieder in die gleiche Richtung wie der erste, er ist nur um das 0,6-fache kürzer.
Das er in die gleiche Richtung zeigt, konnte man erwarten, denn das Vektorprodukt sollte ja einen Normalenvektor für die dargestellte Ebenene sein.

Machen wir weiter mit dem nächsten Vektorprodukt, erleben wir eine Überraschung:

\[ \begin{aligned} \vec{u} \times \vec{v}_6 & = \small{ \begin{pmatrix} 0,4 \\ 1,2 \\ -0,3 \end{pmatrix} \times \begin{pmatrix} -0,4 \\ -1,2 \\ 0,3 \end{pmatrix} } \\ \\ \vec{u} \times \vec{v}_6 & = \small{ \left( \begin{array}{rcr} 1,2 \cdot 0,3 & - & (-0,3)\cdot(-1,2) \\ -0,4\cdot 0,3 & + & (-0,3)\cdot(-0,4) \\ 0,4\cdot(-1,2) & - & 1,2\cdot(-0,4) \end{array} \right) } \\ \\ \vec{u} \times \vec{v}_6 & = \small{ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} } \normalsize{= \vec{0}} \end{aligned} \]

Hier ist das Ergebnis des Vektorprodukts der Nullvektor!
Dieser besondere Vektor hat keine Richtung und seine Länge (sein Betrag) ist null.
Es ist aber ein Vektor (mit drei Komponenten) und nicht eine Zahl. Deshalb wird beim Symbol über der 0 ein Vektorpfeil geschrieben.

Die Vektoren \(\vec{u}\) und \(\vec{v}_6\) bilden einen Winkel von 180° und spannen daher nicht die Ebene auf.
Aus zwei Vektoren, deren Richtungen parallel oder genau entgegen gesetzt zu einander sind, kann man keinen Normalenvektor berechen.
Aber das Vektorprodukt gibt es, s.o.

zurück zur Aufgabe