Lösungshinweise Aufgabe 20
Vorbemerkung:
In dieser Hilfe-Seite wird die erste Methode zum Finden des Normalenvektors gezeigt.
Das ist aber nicht die einzige mögliche.
Die zweite Methode verwendet das Vektorprodukt
und gefällt Ihnen vielleicht besser!
Dazu finden Sie Hinweise bei der nächsten Aufgabe.
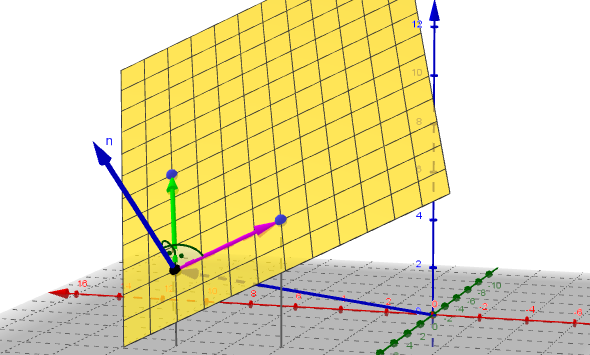
Die Ebene hat die Gleichung \[E: \vec{x} = \left(\begin{matrix}8\\9\\3\end{matrix} \right) + s \cdot \left(\begin{matrix}-4\\-1\\2\end{matrix} \right) + t \cdot \left(\begin{matrix}2\\-5\\3\end{matrix} \right), \; s, t \in \mathbb{R} \]
Da der Vektor \(\vec{n}=\left(\begin{array}{c}n_1\\n_2\\n_3\end{array}\right)\) senkrecht zu beiden Richtungsvektoren stehen soll, müssen die beiden Skalarprodukte 0 ergeben:
\(\left(\begin{array}{c}n_1\\n_2\\n_3\end{array}\right) \cdot \left(\begin{array}{c}-4\\-1\\2\end{array}\right) = 0 \;\) und \(\;\left(\begin{array}{c}n_1\\n_2\\n_3\end{array}\right) \cdot \left(\begin{array}{c}2\\-5\\3\end{array}\right) = 0\)
Multipliziert man beide Skalarprodukte aus, so erhält man die folgenden zwei Gleichungen:
| n1·(−4) | + | n2·(−1) | + | n3·2 | = | 0 |
| n1·2 | + | n2·(−5) | + | n3·3 | = | 0 |
| I |
| II |
oder
| −4 n1 | − | n2 | + | 2 n3 | = | 0 |
| 2 n1 | − | 5 n2 | + | 3 n3 | = | 0 |
| I |
| II ⇔ |
| −4 n1 | − | n2 | + | 2 n3 | = | 0 |
| 4 n1 | − | 10 n2 | + | 6 n3 | = | 0 |
| I |
| II ·2 ⇔ |
| −4 n1 | − n2 | + | 2 n3 | = | 0 | |
| −11 n2 | + | 8 n3 | = | 0 |
| I |
| II+I |
Das Gleichungssystem hat 3 Unbekannte (die Komponenten von
\(\vec{n}\)), aber es gibt nur 2 Gleichungen.
Deshalb gibt es keine eindeutige Lösung.
Die zweite Gleichung enthält noch zwei Unbekannte.
Eine davon kann man nun beliebig festlegen.
Wenn wir für n3
einen Wert festlegen, sollten wir es uns nicht zu schwer machen:
Weil beim Auflösen nach n2
durch 11 geteilt werden muss, ist es besonders günstig, wenn
die Wahl
\(n_3 = 11\)
getroffen wird.
Dann folgt danach, dass \(n_2 = 8\) ist.
Die beiden Werte werden nun in die erste Gleichung eingesetzt und man berechnet damit \(n_1 = \frac{7}{2}=3,5\)
Damit ist
\(\vec{n}=\left(\begin{array}{c}3,5\\8\\11\end{array}\right)\).
In der Zeichnung oben wurde der Vektor halb so lang angesetzt,
damit er besser in die Zeichnung hinein passt. An seiner Richtung
ändert das natürlich nichts.
Zur Probe können Sie beide Skalarprodukte aus diesem Normalenvektor und einem Richtungsvektor der Ebene ausrechen: Es sollte 0 heraus kommen, da beide Male ein rechter Winkel vorliegt.