Lösungshinweise Aufgabe 19

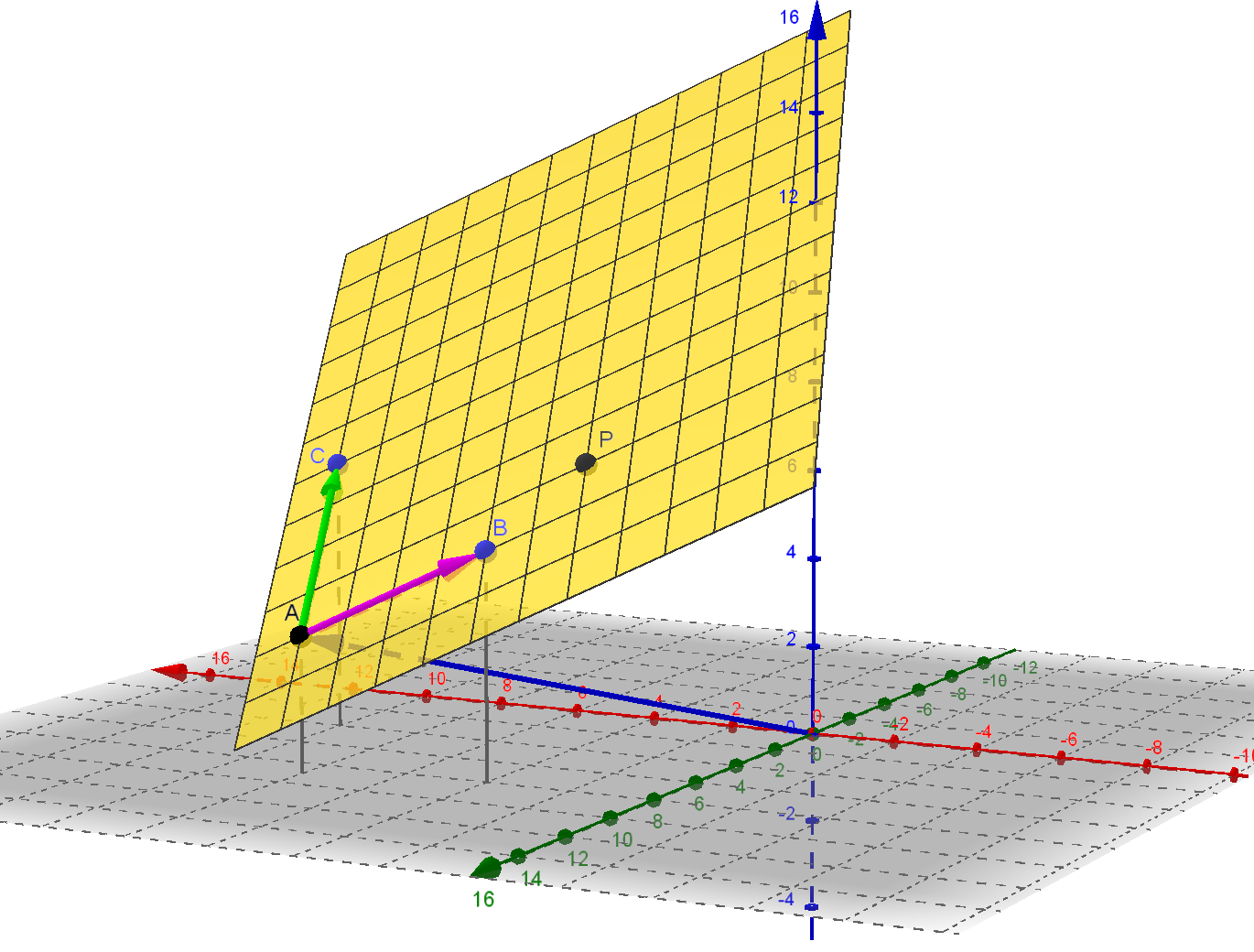
Abbildung: Ebene_1 im Raum

Die Ebene hat die Gleichung \[E: \vec{x} = \left(\begin{matrix}8\\9\\3\end{matrix} \right) + s \cdot \left(\begin{matrix}-4\\-1\\2\end{matrix} \right) + t \cdot \left(\begin{matrix}2\\-5\\3\end{matrix} \right), \; s, t \in \mathbb{R} \]

Da der Schnittpunkt S dieser Ebene mit der z-Achse gesucht ist, haben wir zwei Informationen über S:
S liegt auf der Ebene, seine Koordinaten erfüllen also die Ebenengleichung.
S liegt auf der z-Achse.

Doch was ist das besondere an allen Punkten auf der z-Achse?

Bei allen Punkten auf der z-Achse ist die x- und die y-Koordinate 0.
Das bedeutet, dass für den Ortsvektor des gesuchten Punkts S gelten muss: \[\vec{x}_S = \left(\begin{matrix}0\\0\\z\end{matrix} \right) = \left(\begin{matrix}8\\9\\3\end{matrix} \right) + s \cdot \left(\begin{matrix}-4\\-1\\2\end{matrix} \right) + t \cdot \left(\begin{matrix}2\\-5\\3\end{matrix} \right)\]

Diese Vektor-Gleichung besteht aus drei Gleichungen:

 0 = 8 + s·(−4) + t·2
 0 = 9 + s·(−1) + t·(−5)
 z = 3 + s·2 + t·3
I
II
III

oder

−4 s + 2 t = −8
−s − 5 t = −9
 2 s + 3 t − z = −3
I
II   ⇔
III
−4 s + 2 t = −8
4 s + 20 t = 36
 2 s + 3 t − z = −3
I
II·(−4)   ⇔
III
−4 s + 2 t = −8
22 t = 28
 2 s + 3 t − z = −3
I
II + I
III

Aus der zweiten Gleichung folgt nun, dass t = 28/22 = 14/11 ist.
Setzt man diesen Wert in die Gleichung I ein, so erhält man s = 29/11.

Diese Werte für s und t werden nun in die dritte Gleichung eingesetzt, um z zu berechnen.

Mit diesem Wert für z können Sie dann den Schnittpunkt S angeben, sie finden ihn bei den Lösungsvorschlägen zur Aufgabe unter A, B, C oder D.

Bevor Sie das Gleichungssystem ähnlich wie eben gezeigt von Hand lösen, denken Sie auch daran, dass es vielleicht schneller mit dem Taschenrechner geht.
Einen Hinweis dazu habe ich schon in Aufgabe 3 und in der Übersichtsseite gegeben:
Casio FX991, Lineare Gleichungssysteme mit Casio 991

zurück zur Aufgabe