Lösungshinweise Aufgabe 17
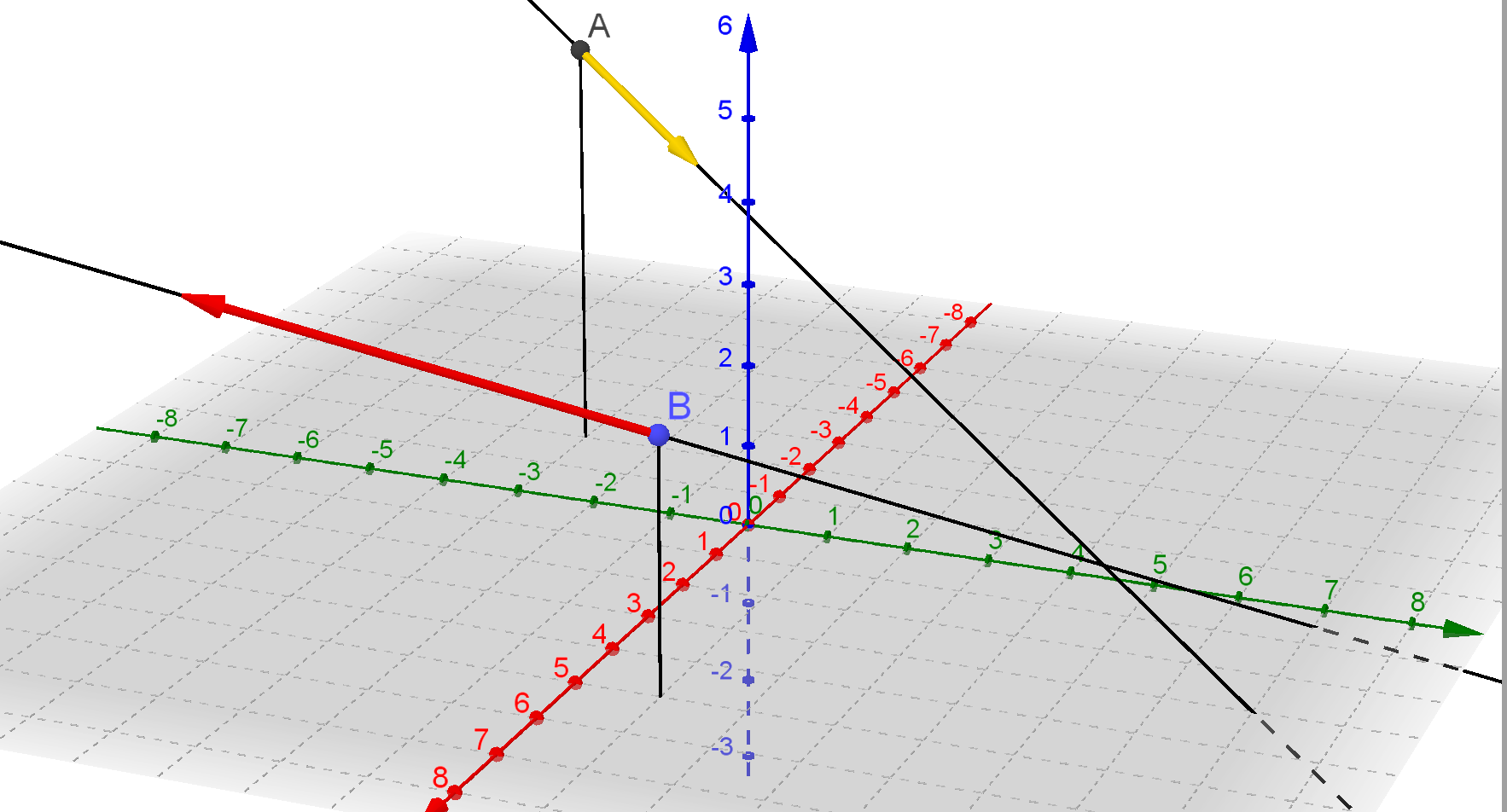
Die Geraden haben die Gleichungen \[ \begin{align} g: \vec{x} &= \left(\begin{matrix}-2\\-3\\5\end{matrix} \right) + s \cdot \left(\begin{matrix}1\\2\\-1\end{matrix} \right) \; s \in \mathbb{R} \\ h: \vec{x} &= \left(\begin{matrix}5\\1\\3\end{matrix} \right) + t \cdot \left(\begin{matrix}3\\-4\\2\end{matrix} \right) \; t \in \mathbb{R} \end{align}\]
Wir nehmen zunächst an, dass ein Schnittpunkt existiert.
Wenn sich bei der Berechnung dieses Schnittpunktes ein Widerspruch
ergibt, wissen wir, dass kein solcher existiert und die Geraden
windschief sind.
Für den Schnittpunkt muss es sowohl eine Darstellung in der Form
der Geraden g als auch in der Form der Geraden h geben.
Beide Darstellungen müssen also zum selben Punkt führen, deshalb
dürfen wir sie gleichsetzen:
\[
\left(\begin{matrix}-2\\-3\\5\end{matrix} \right)
+ s \cdot \left(\begin{matrix}1\\2\\-1\end{matrix} \right)
=
\left(\begin{matrix}5\\1\\3\end{matrix} \right)
+ t \cdot \left(\begin{matrix}3\\-4\\2\end{matrix} \right)
\]
Diese Vektor-Gleichung besteht aus drei Gleichungen:
(Versuchen Sie selbständig weiter zu rechnen, sobald Sie beim Lesen verstanden haben, wie es weiter geht ...)
| −2 | + | s·1 | = | 5 | + | t·3 | I |
| −3 | + | s·2 | = | 1 | + | t·(−4) | II |
| 5 | + | s·(−1) | = | 3 | + | t·2 | III |
oder
| s | − | 3 t | = | 7 | I | |
| 2s | + | 4 t | = | 4 | II | ⇔ |
| −s | + | −2 t | = | −2 | III |
| s | − | 3 t | = | 7 | I | |
| 10 t | = | −10 | II + I·(-2) | ⇔ | ||
| −5 t | = | 5 | III + I |
| s | − | 3 t | = | 7 | I |
| t | = | −1 | II : 10 | ||
| t | = | −1 | III : (−5) |
Da die letzten Gleichungen beide zum selben Wert für
t führen,
existiert ein Schnittpunkt.
Setzen Sie den Wert von t in Gleichung I ein,
um den Wert von s zu erhalten.
Setzen Sie zum Schluss den Wert von t
in die zweite Geradengleichung ein, so erhalten Sie den Ortsvektor
des Schnittpunktes.
Zur Kontrolle/Probe können Sie noch den Wert von s
in die erste Geradengleichung einsetzen: Das Ergebnis sollte das gleiche sein.
Denken Sie zum Schluss noch daran, einen kleinen Antwortsatz zur Lagebeziehung von g und h zu formulieren und den Schnittpunkt korrekt in Punktdarstellung (und nicht als Vektor) anzugeben.