Lösungshinweise Aufgabe 15
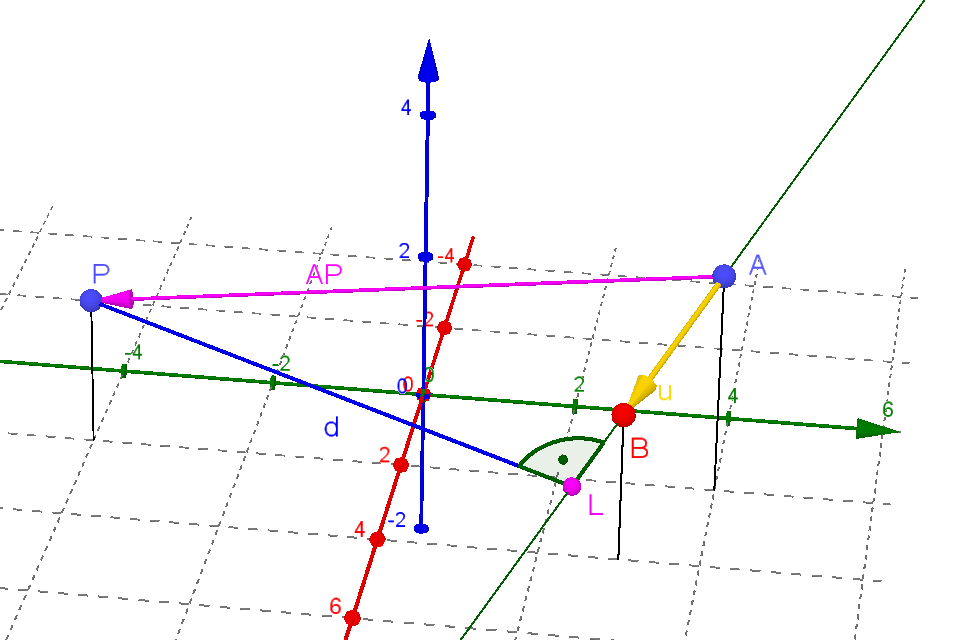
Mit Hilfe des ersten Hinweises könnten Sie für den Vektor
\(\overrightarrow{OL}\) folgendes notiert haben:
\(
\begin{aligned}
\overrightarrow{OL}
& =
\overrightarrow{OA} +
t \cdot \overrightarrow{AB}
\\
\overrightarrow{OL}
& =
\vec{a} +
t \cdot \vec{u} \quad
\end{aligned}
\),
Mit
A = ( 2 ∣ 4 ∣ 3 )
und
B = ( 4 ∣ 3 ∣ 2 )
also
\(
\overrightarrow{OL}
=
\small{\left(\begin{matrix}2\\4\\3\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\)
Mit
\(
\overrightarrow{OP}=
\vec{p}=
\small{\left(\begin{matrix}2\\-4\\2\end{matrix}\right)}
\)
erhält man dann für den Vektor von P nach L
\(
\begin{aligned}
\vec d =
\overrightarrow{PL}
& =
\overrightarrow{OL}
-
\overrightarrow{OP}
\\
\\
\vec d =
\overrightarrow{PL}
& =
\small{\left(\begin{matrix}2\\4\\3\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\normalsize{ ~-~ }
\small{\left(\begin{matrix}2\\-4\\2\end{matrix}\right)}
\\
\\
\vec d =
\overrightarrow{PL}
& =
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\end{aligned}
\)
Dieser Vektor \(\vec{d}\) soll minimale Länge haben.
Je kürzer der Vektor ist, desto kleiner ist auch das Quadrat
der Länge. Deshalb wird das Quadrat untersucht:
\(
\begin{aligned}
\vert \vec{d} \vert^2
& =
\vec{d} \cdot \vec{d}
\\
\vert \vec{d} \vert^2
& =
\left[
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\right]
\cdot
\left[
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\right]
\\
\\
\vert \vec{d} \vert^2
& =
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}^{\normalsize{2}}
\normalsize{ ~+~ 2 \cdot}
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\normalsize{ \cdot t}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\normalsize{ ~+~ t^2}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}^{\normalsize{2}}
\\
\\
\vert \vec{d} \vert^2
& =
65 ~+~ 2 t
\cdot (-9) ~+~ t^2 \cdot 6
\end{aligned}
\)
Mit den bekannten Methoden aus der ANALYSIS können Sie nun bestimmen,
an welcher Stelle das Minimum der Funktion
\(f(x) = 6 x^2 - 18 x + 65 \) liegt.
Mit diesem Wert für den Parameter \(t\) liefert die Geradengleichung
die Lage des Punktes L.