Lösungshinweise Aufgabe 15
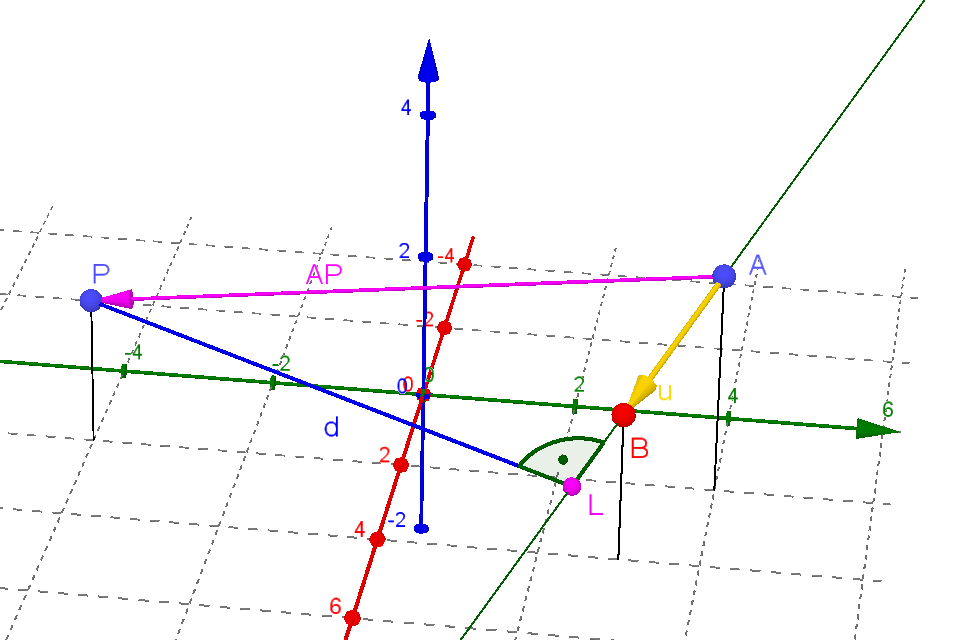
Mit Hilfe des ersten Hinweises könnten Sie für den Vektor
\(\overrightarrow{OL}\) folgendes notiert haben:
\(
\overrightarrow{OL}
=
\overrightarrow{OA} +
t \cdot \overrightarrow{AB}
\)
oder
\(
\overrightarrow{OL}
=
\vec{a} +
t \cdot \vec{u}
\),
mit
A = ( 2 ∣ 4 ∣ 3 )
und
B = ( 4 ∣ 3 ∣ 2 )
also
\(
\overrightarrow{OL}
=
\small{\left(\begin{matrix}2\\4\\3\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\)
Wegen
P = ( 2 ∣−4 ∣ 2 )
ist
\(
\overrightarrow{OP}=
\vec{p}=
\small{\left(\begin{matrix}2\\-4\\2\end{matrix}\right)}
\), damit
erhält man für den Vektor von P nach L
\(
\begin{aligned}
\vec{d}
=
\overrightarrow{PL}
& =
\overrightarrow{OL}
-
\overrightarrow{OP}
\\
\\
\vec{d}
=
\overrightarrow{PL}
& =
\small{\left(\begin{matrix}2\\4\\3\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\normalsize{ ~-~ }
\small{\left(\begin{matrix}2\\-4\\2\end{matrix}\right)}
\\
\\
\vec{d}
=
\overrightarrow{PL}
& =
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\end{aligned}
\)
Dieser Vektor soll senkrecht zum Richtungsvektor
\(
\vec{u}
=
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\)
der Geraden stehen, also \(\vec{d} \cdot \vec{u} =0\), d.h.
\(
\left[
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\right]
~\cdot~
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
~ = ~
0
\)
Nun brauchen Sie nur noch auszumultiplizieren:
\(
\small{\left(\begin{matrix}0\\8\\1\end{matrix}\right)}
\cdot
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\normalsize{ ~+~ t ~ \cdot}
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
\cdot
\small{\left(\begin{matrix}2\\-1\\-1\end{matrix}\right)}
~ = ~
0
\)
Nach dem Ausrechnen der beiden Skalarprodukte
erhalten Sie eine einfache Gleichung für t.
Berechnen Sie t und setzen Sie diesen Wert in die
Geradengleichung ein.