Lösungshinweise Aufgabe 15
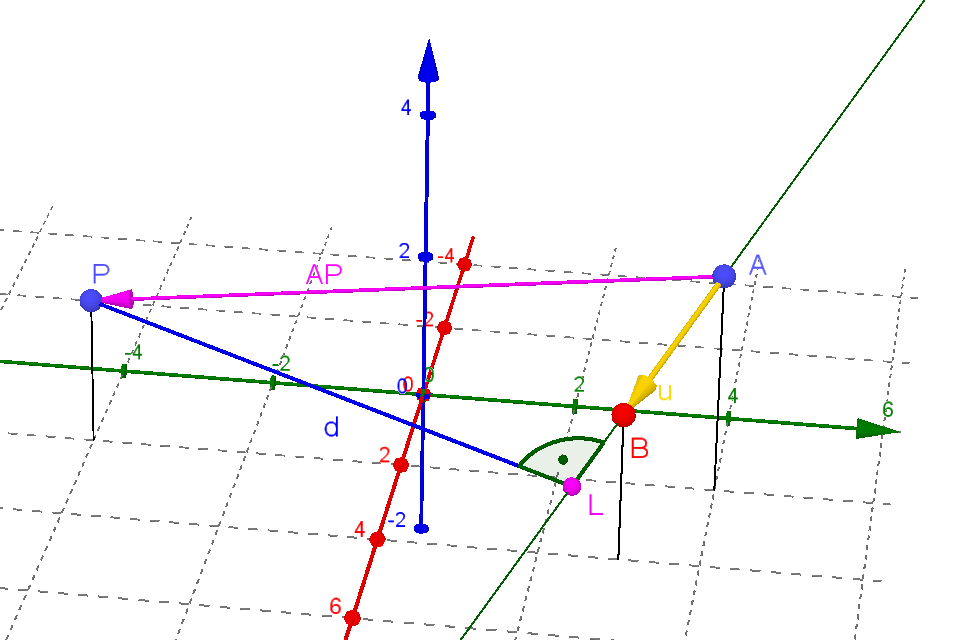
Gesucht ist der Punkt L, für den die Verbindungsstrecke von P nach L
senkrecht zur Geraden g steht.
Diese Verbindungsstrecke wird durch den Vektor
\(\overrightarrow{PL}\) dargestellt, und es gilt
\(\overrightarrow{PL} = \overrightarrow{OL} - \overrightarrow{OP} \quad (I) \).
L ist zwar nicht bekannt, aber man weiß, dass L auf der Geraden g
liegt. Also ergibt sich der Ortsvektor von L mit einem ganz
bestimmten Wert für den Parameter \(t\) in der Geradengleichung von g.
\(
\begin{aligned}
\overrightarrow{OL}
& =
\overrightarrow{OA} +
t \cdot \overrightarrow{AB}
\\
\overrightarrow{OL}
& =
\vec{a} +
t \cdot \vec{u} \quad (II)
\end{aligned}
\)
Die Komponenten der Vektoren \(\vec{a}\) (Stützvektor)
und \(\vec{u}\) (Richtungsvektor) sind Ihnen durch die gegebenen
Punkte
A = ( 2 ∣ 4 ∣ 3 )
und
B = ( 4 ∣ 3 ∣ 2 )
bekannt. Lassen Sie nur den Parameter \(t\) als Unbekannte stehen.
Da P = ( 2 ∣ −4 ∣ 2 ) gegeben ist, ist natürlich auch der Ortsvektor von P bekannt, nämlich \( \overrightarrow{OP}= \vec{p}= \small{\left(\begin{matrix}2\\-4\\2\end{matrix}\right)} \quad (III) \)
Setzen Sie die Terme aus (II) und (III) in (I) ein, um einen Ausdruck
für den Vektor
\(\vec{d} = \overrightarrow{PL}\)
von P nach L zu erhalten.