Lösungshinweise Aufgabe 14
Gesucht ist der Abstand d des Punktes P von der Geraden g. Ein Formel zur Berechnung dieses Abstands lautet: \[ d = \sqrt{ \overrightarrow{AP} \cdot \overrightarrow{AP} - \frac { ( \vec{u} \cdot \overrightarrow{AP} )^2} {\vec{u} \cdot \vec{u}} } \] oder anders geschrieben \[ d = \sqrt{ {\vert{\overrightarrow{AP} } \vert}^2 - \frac { ( \vec{u} \cdot \overrightarrow{AP} )^2} {\vert{\vec{u}\vert}^2} } \]
Diese Formel ist recht einfach zu verwenden, denn man braucht für die
auftretenden Beträge von Vektoren keine Wurzeln zu ziehen, da diese
Beträge ja nur quadriert vorkommen.
Beachten muss man aber, dass auch das Skalarprodukt im Zähler des Bruches
quadriert wird.
Beweis für die Formel
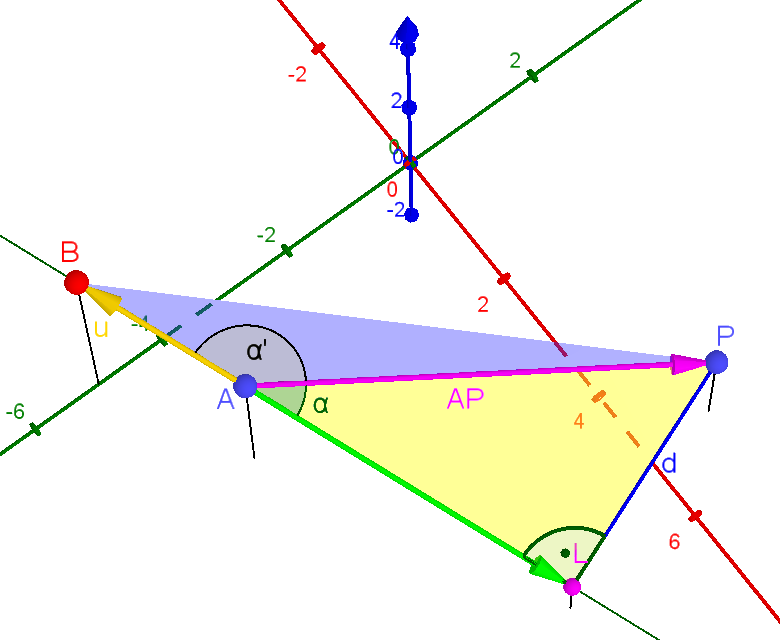
Wir beginnen mit der letzten Formel aus Hinweis 1
zu dieser Aufgabe:
\[ \begin{aligned}
\sin(\alpha) & = \frac{d}{
\vert {\overrightarrow{AP}} \vert }
& (I)
\\
d^{~2} & = {\vert {\overrightarrow{AP}} \vert}^2 \cdot \sin^2(\alpha)
& (II)
\\
d^{~2} & = {\vert {\overrightarrow{AP}} \vert}^2 \cdot \left(1 - \cos^2(\alpha)\right)
& (III)
\end{aligned}\]
Nun ist aber \(\cos^2(\alpha) = \cos^2(\alpha~') \),
denn \(\cos(180°-\alpha) = - \cos(\alpha) \), und das Minuszeichen verschwindet
beim Quadrieren.
Das bedeutet, dass es egal ist, ob der Vektor \(\vec{u}\) von A aus zum
Lotfußpunkt L hin zeigt oder in die entgegengesetzte Richtung.
Wegen
\(
\cos^2(\alpha) = \cos^2(\alpha~')
=
\frac
{\vec{u} \cdot \overrightarrow{AP}}
{\vert \vec{u}\vert \cdot \vert \overrightarrow{AP} \vert}
\)
wird nun dieser Bruch in \((III)\) eingesetzt:
\[ \begin{aligned}
d^{~2}
& ~=~
{\vert {\overrightarrow{AP}} \vert}^2
\cdot
\left(1 - \cos^2(\alpha)\right)
& (IV)
\\
d^{~2}
& ~=~
{\vert {\overrightarrow{AP}} \vert}^2
\cdot
\left(1 - \frac
{( \vec{u} \cdot \overrightarrow{AP} )^2}
{( \vert \vec{u}\vert \cdot \vert \overrightarrow{AP} \vert )^2}
\right)
& (V)
\\
d^{~2}
& ~=~
{\vert {\overrightarrow{AP}} \vert}^2
- \frac
{( \vec{u} \cdot \overrightarrow{AP} )^2}
{\vert \vec{u}\vert ^2}
& (VI)
\\
d
& ~=~
\sqrt{
{\vert{\overrightarrow{AP} } \vert}^2 -
\frac
{ ( \vec{u} \cdot \overrightarrow{AP} )^2}
{\vert{\vec{u}\vert}^2}
}
& \text{q.e.d.}
\end{aligned}\]