Lösungshinweise Aufgabe 14
Gesucht ist der Abstand d des Punktes P von der Geraden g.
Dazu wird das gelbe Dreieck ALP betrachtet:
Welche Größen in diesem Dreieck sind bekannt?
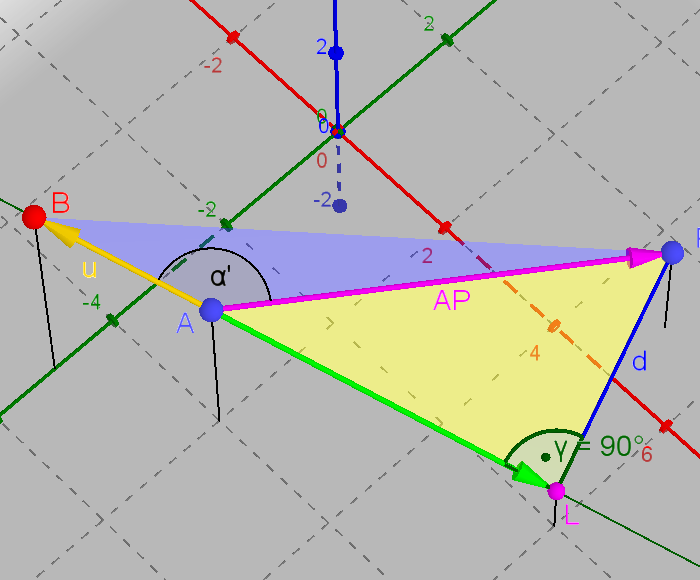
Die Strecke, die den gesuchten Abstand darstellt, muss senkrecht
zu g stehen, damit sie die kürzeste Verbindung von P zu g ist.
Bei L liegt also ein rechter Winkel.
Da die Koordinaten von A und P bekannt sind, lässt sich auch die
Länge der Seite AP berechnen.
Die Koordinaten des Lotfußpunktes
L sind nicht ganz einfach
zu berechen, aber sie werden gar nicht gebraucht!
Bestimmen Sie stattdessen den Winkel α =∡(P,A,L) bei A!
Dazu berechnen Sie zunächst den den Winkel α' mit dem Skalarprodukt:
\[
{\vec{u} \cdot \overrightarrow{AP}}
=
{ {\left| \vec{u} \right| } \cdot
{ \vert {\overrightarrow{AP}} \vert }
\cdot \cos(\alpha~')
} \quad\quad (I) \]
Mit A = ( 2 | −4 | 3 ) und B = ( 0 | −5 | 4 ) hat die Gerade g die Gleichung \(g: \vec{x} = \left(\begin{matrix}2\\-4\\3\end{matrix} \right) + t \cdot \left(\begin{matrix}-2\\-1\\1\end{matrix} \right), \; t \in \mathbb{R} \), und \( \vec{u} = \left(\begin{matrix}-2\\-1\\1\end{matrix} \right) \) ist Richtungsvektor der Geraden.
Mit P = (5|1|2) ist \(\overrightarrow{AP} = \left(\begin{matrix}3\\5\\1\end{matrix} \right) \), und eingesetzt in \((I)\) ergibt sich
\[ \begin{aligned} \small{ \left(\begin{matrix}-2\\-1\\1\end{matrix} \right)\cdot\left(\begin{matrix}3\\5\\1\end{matrix} \right)} \normalsize &= \small{ \left|{\left(\begin{matrix}-2\\-1\\1\end{matrix} \right)}\right| \cdot \left|{\left(\begin{matrix}3\\5\\1\end{matrix} \right)}\right| } \normalsize{ \cdot \cos(\alpha~')} &(II) \\ \\ -10 ~&=~ \sqrt{6} \cdot \sqrt{35} \cdot \cos(\alpha~') &(III) \end{aligned} \]
Aus \((III)\) können Sie nun α' berechnen, dann α, und mit
\[ \begin{aligned} \quad\sin(\alpha) &= \frac{d}{ \vert {\overrightarrow{AP}} \vert } & \quad\quad\quad\quad\quad\quad (IV) \end{aligned}\]
kommen Sie zum gesuchten Wert für den Abstand d.