Herleitung zum Vektorbetrag
Zunächst projizieren wir die Punkte A und B senkrecht auf die x-y-Ebene und betrachten den Abstand dieser beiden Punkte:
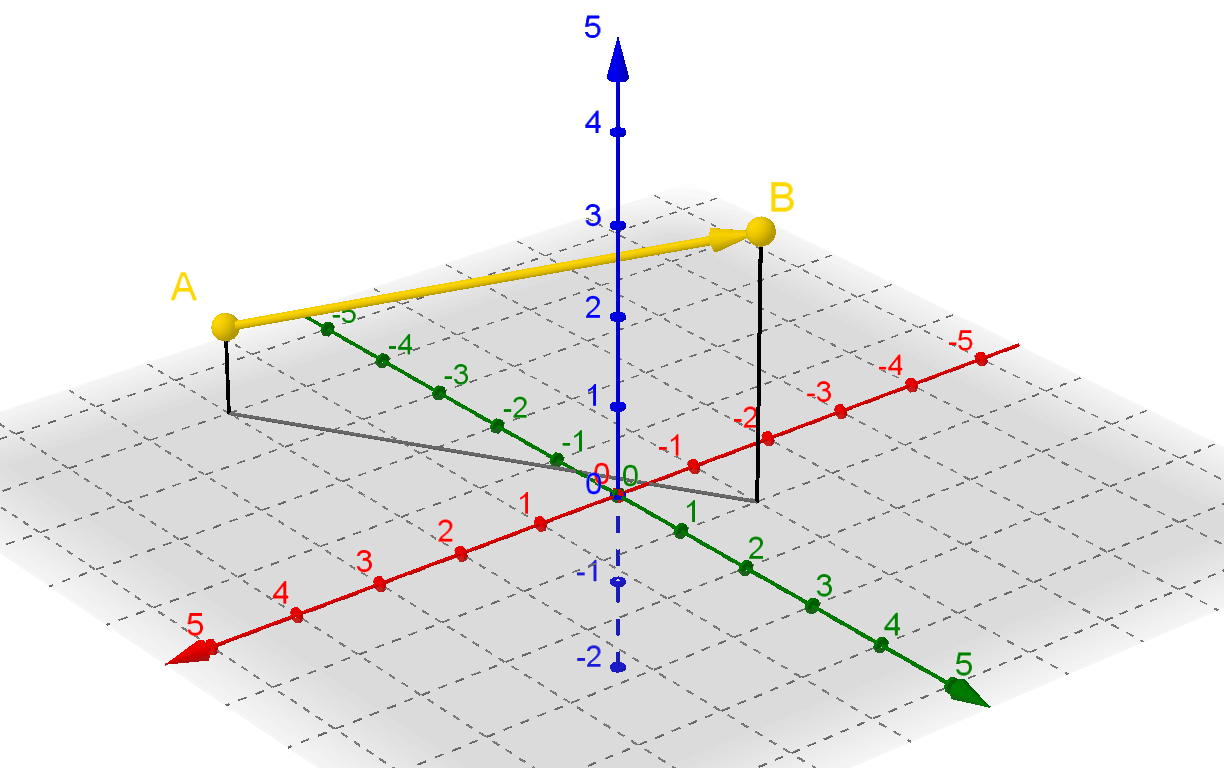
Dieser Abstand lässt sich mit Hilfe des Satzes von Pythagoras berechnen:
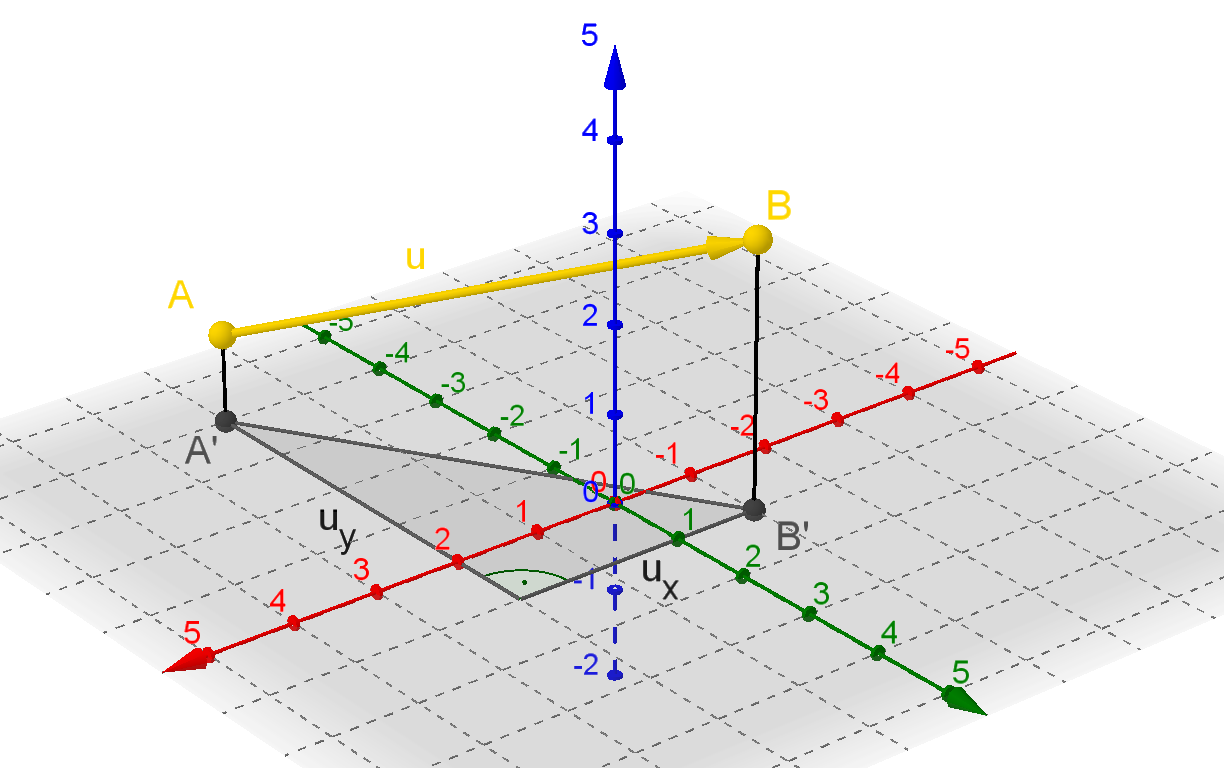
Die Katheten des rechtwinkligen Dreiecks in der x-y-Ebene haben als
Längen die x- bzw. y-Komponente des Vektors \(\vec{u}\).
Somit haben die Punkte A' und B' voneinander den Abstand
\(\sqrt{ {u_x}^2 + {u_y}^2 }\), hier im Beispiel also
\(\sqrt{ (-3)^2 + 5^2 } = \sqrt{34}\).
Anmerkung:
Die x-Komponente des Vektors \(\vec{u}\) ist −3, also negativ.
Im eingezeichneten Dreieck hat die zugehörige Kathete die
vorzeichenlose Länge 3.
Das Quadrat der Länge ist ebenso wie das Quadrat der negativen x-Komponente
positiv. Die Vorzeichen der Komponenten des Vektors haben also keinen
Einfluss auf die Länge des Vektors.
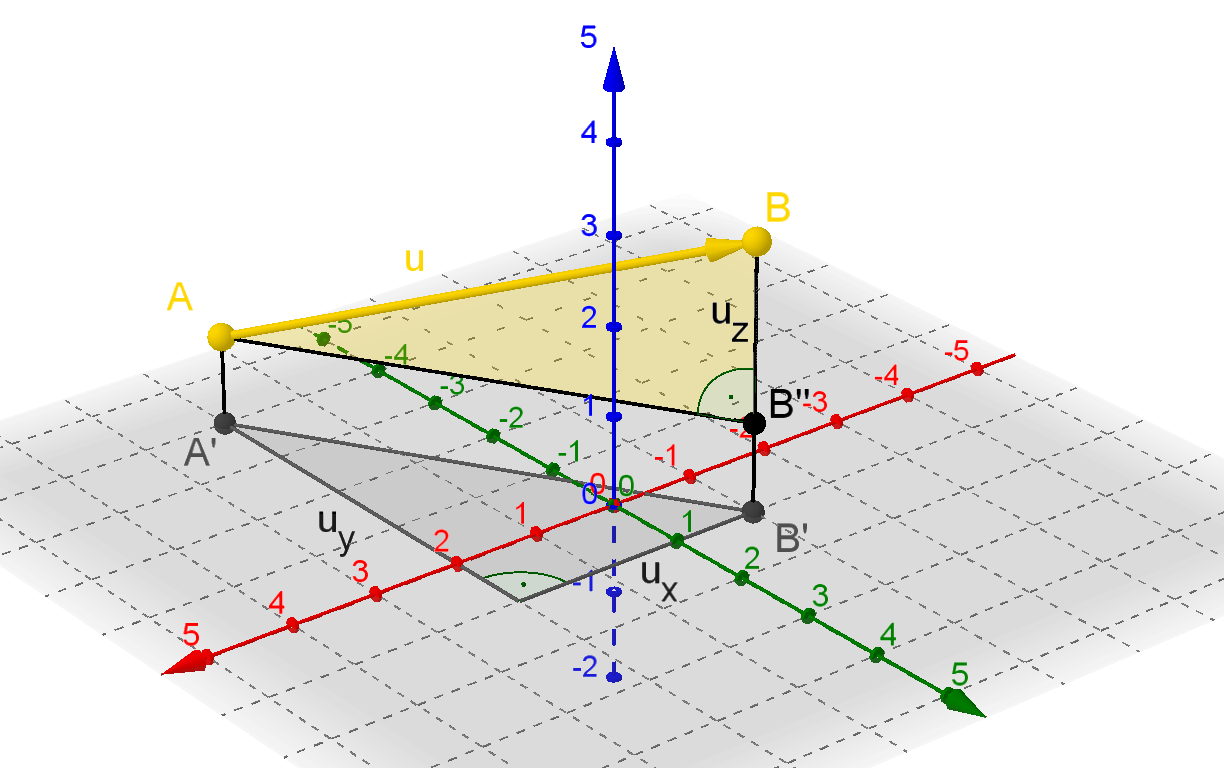
Der Abstand von A nach B'' ist genauso groß wie der Abstand von A' nach B'
Damit lässt sich nun die Länge des Vektors
\(\vec{u} = \overrightarrow{AB}\)
berechnen:
Die eine Kathete hat die Länge \(\sqrt{ {u_x}^2 + {u_y}^2 }\), die andere hat die Länge \(u_z\). Nach dem Satz des Pythagoras gilt demnach \[ |\vec{u}|^2 = \left( \sqrt{ {u_x}^2 + {u_y}^2 }\right)^2 + {u_z}^2 \] also \[ |\vec{u}|^2 = {u_x}^2 + {u_y}^2 + {u_z}^2 \] und somit \[ |\vec{u}| = \sqrt{{u_x}^2 + {u_y}^2 + {u_z}^2} \]
Für den Vektor im Beispiel gilt dann \[ |\vec{u}| = \left| \left( \begin{array} {c} -3 \\ 5 \\ 2 \end{array} \right) \right| = \sqrt{ (-3)^2 + 5^2 + 2^2 } = \sqrt{38} \approx 6,164 \]
Der Vektor \(\vec{u}\) hat also eine Länge von ungefähr 6,16 Längeneinheiten.